Room temperature superconductivity is hard. LK-99 illustrates why

In our conventional lives, we’re all familiar with electricity: where charged particles move through a complete circuit, and where that electrical energy can be used to power all sorts of devices. Whenever you have a conventional electrical current — caused by the motion of charged particles — one of only two things are typically happening. Either the electrons within a material are being forced through the entire material, both on the surface and on the interior, or they’re all traveling exclusively on the surface of the material. When electrons move only on the surface, that’s evidence that you have a conductor; when electrons move all throughout the material, those are the properties of an insulator, or a material with low conductivity/high resistivity.

But some materials behave fundamentally differently from both insulators and conductors: superconductors. Whereas moving charged particles create magnetic fields and magnetic fields, in turn, influence the movement of charged particles, superconductors are instead defined by two remarkable properties:

1. all internal magnetic fields are 100% expelled from within a superconductor,
2. and the electrical resistance of the material drops perfectly and completely away, exactly to zero.

With the recent hype surrounding the material LK-99, a purported (and unconfirmed) room-temperature superconductor, superconductivity has been all over the news. But there are no known room temperature superconductors at present, including LK-99, and there are some compelling physics reasons for it that everyone should know.

This simulation shows particles in a gas of a random initial speed/energy distribution colliding with one another, thermalizing, and approaching the Maxwell-Boltzmann distribution. The state of reaching thermal equilibrium is when all parts of the system can exchange energy, collide with, and interact with all other parts of the system freely, and is easy to achieve for a closed, isolated, unchanging system. By contrast, the expanding Universe is wildly out of equilibrium.

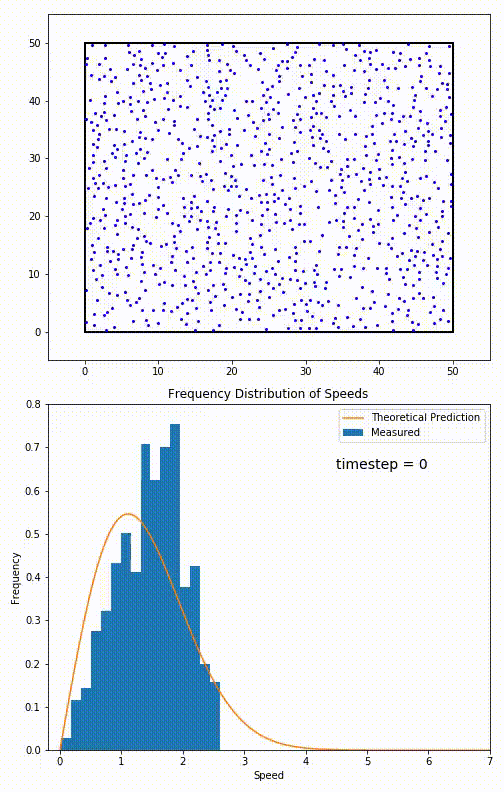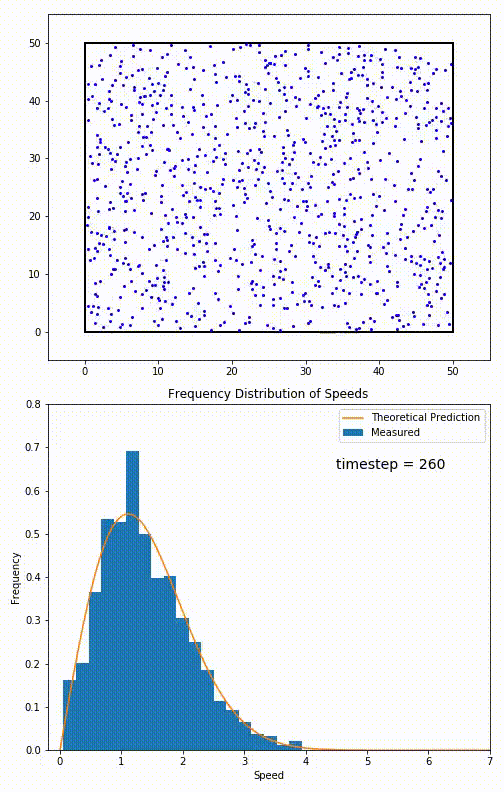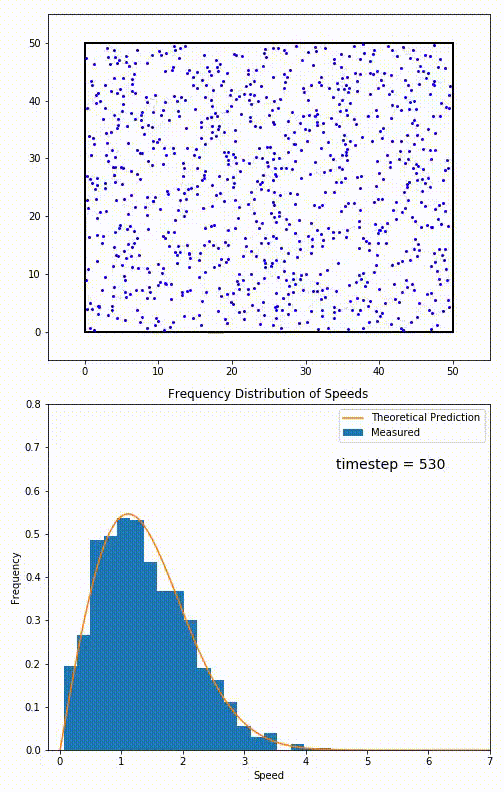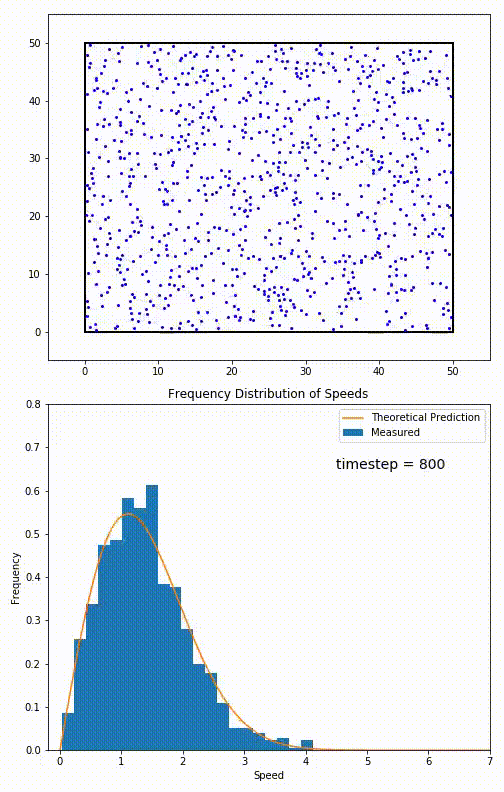
Maybe the best place to start is not with any electric or magnetic phenomena, but simply the idea of particles that occupy a volume of space. Under conventional conditions — i.e., room temperature and ambient pressures — each particle within this volume will move around and, after traveling for a certain amount of time, will smash into another particle, at which point energy and momentum are exchanged between them.

Over time, these particles will come to reach what’s known as an equilibrium state: where all of the particles within it obey a Bell curve (or, more precisely, a Maxwell-Boltzmann distribution) in terms of their energy. No part of this system will have more energetic or less energetic particles than average; the system will be in thermal equilibrium.

If you want your particles to smash into one another (i.e., collide) less frequently, you must either:

• lower the temperature of the system,
• take particles out of the system,
• increase the volume of the system,
• or set up some special sort of conditions that prevents particles from colliding with one another.

Any one of these modifications can lead to a system where particles interact less frequently, increasing what’s known as their “mean free path.”

If you wanted your particles, however, to not collide at all, you’d have to go to extreme measures.

Electrical resistance is not a fundamental property of a material, but rather is related to resistivity, the length of the material (l), and the cross-sectional area (A) of the material. Resistivity is temperature-dependent, with higher temperatures leading to greater resistivity and lower temperatures leading to less. However, the purely quantum phenomenon of superconductivity can sometimes lead the resistivity of a material to drop to zero below a critical temperature, enabling a truly resistance-free system.

For a gas of moving particles, you’d need to lower the temperature all the way to absolute zero: to take all of the motion out of these particles entirely. Barring that, you could remove particles until only a single one remained in your system: with nothing else for it to interact with. Alternatively, you could increase the volume to be infinitely large, expanding the space between particles so that they could free-stream forever without smashing into another one.

However, inside of a material, it’s possible to coax them into another specific set of circumstances. That circumstance would be:

• where you have a series of low-energy states that are all stable and fully occupied,
• where you have a remaining, higher-energy state that all of your remaining particles will spontaneously fall into,
• where those particles behave not like fermions, which cannot occupy identical quantum states in the same place at the same time, but rather like bosons, where there is no limit to how many of them can occupy the same quantum state,
• and where those particles will remain in that state, rather than transitioning upward to higher-energy ones or downward to lower-energy ones.

This isn’t science-fiction that such a state would exist; it’s an essential part of the science of condensed matter physics.

The three conventional types of materials are conductors, semiconductors, and insulators, which are typically defined by the size of the energy gap between the valence band and the conduction band. Conductors have no gaps between them, while semiconductors and insulators have them. If electrons fully occupy the valence bands but do not reach the conduction band yet still rise above the edge of the valence band, that is when superconductivity becomes possible. If temperatures rise high enough that the conduction band is reached, superconductivity will not occur.

Coaxing the most common of electricity-carrying particles, the electron, into a specific state is difficult; coaxing it to make a specific transition 100% of the time is an even greater challenge. That’s part of the reason why LED lights were around for so long — more than 30 years, in fact — before it became possible to produce the full spectrum of colors with them. When electrons transition from one state to another, they emit photons of a particular wavelength that corresponds to the energy difference between those two states. In the case of a light-emitting diode, getting energy differences that corresponded to red, yellow, and green wavelengths of light were easy, but the first blue LED was not invented until 1994!

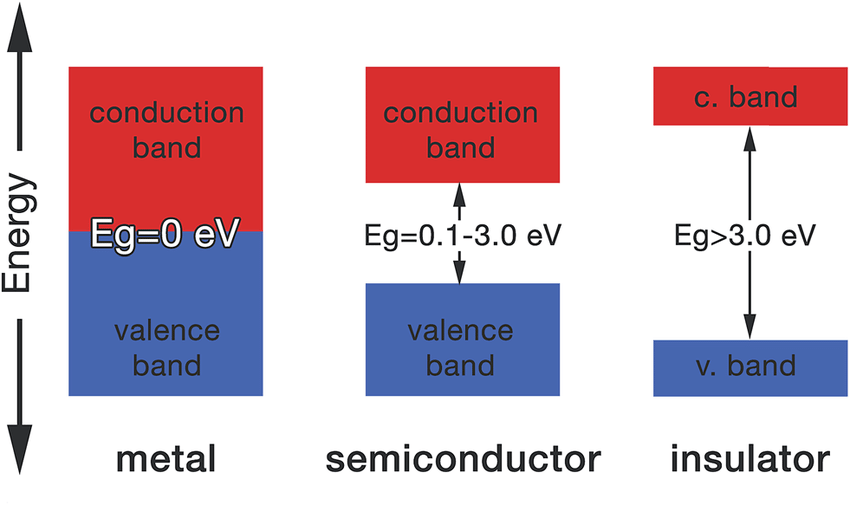
In order to achieve a superconducting state in a material, the basic thing that you need, universally, is an energy gap in the spectrum that electrons can occupy. This way, the lower-energy states, the ones below the gap, would be 100% filled by the material’s electrons; they’d be completely occupied. If you tried to push these electrons through the material, they couldn’t do it without encountering the resistance of the other electrons within that band. In fact, not only would your material not superconduct, but it wouldn’t conduct at all. Trying to move electrons through an electron-rich material where the electrons aren’t “free” is how you get an insulator, and this describes the behavior of most materials under most conditions.

This diagram shows a cutaway of the interior of a coaxial cable. With current flowing in one direction down the central, interior cable and the opposite direction down the outer cable, these boundary conditions enable the propagation of an internal “transverse electric-and-magnetic” mode in the space between the conductors. This configuration, known as TEM, can only arise due to the specific boundary conditions present in a coaxial cable-like system. This is for a normal conductor, where all of the charge is transported along the surface.

However, what if — above those occupied energy states, known as the valence band — you have a set of energy states that are all at approximately the same energy, and at the same time, they’re all unpopulated?

That’s what we call a “band” of energy states, and specifically, a near-continuous collection of energy states that it’s possible for an electron to occupy. If the band is empty and unpopulated except for your one electron of interest, it can move freely across it: that’s what we call a conduction band. That’s the key to making a conductor: a band of energy states that the electron can propagate through without encountering the resistance of other electrons occupying that same band. The more “holes” (i.e., unpopulated states) there are in your band, the better of a conductor it becomes, and the less resistivity the material you’re considering will display.

The big difference between a conductor and a superconductor is simply this: in a normal conductor, the largely unpopulated states contain electrons, which are fermions that obey the Pauli exclusion principle. Each electron must occupy a different quantum state than every other electron that overlaps with its location at each moment in time, which means that it can only transition to a free, unpopulated state that doesn’t already have an electron in it. Because electric current is always carried by more than one electron in practice, even the best conductors always have at least some non-zero amount of resistance to them.

The left-hand side of the diagram illustrates the formation of Cooper pairs. At top, a traveling electron attracts and distorts the positive charges within the underlying lattice, which preferentially attracts a second electron (left-bottom), allowing those two electrons to form a Cooper pair. At right, a gap in the energy levels allows the existence of a superconducting state (blue line), but no gap, and no superconductivity, is displayed by a standard metal (red line).

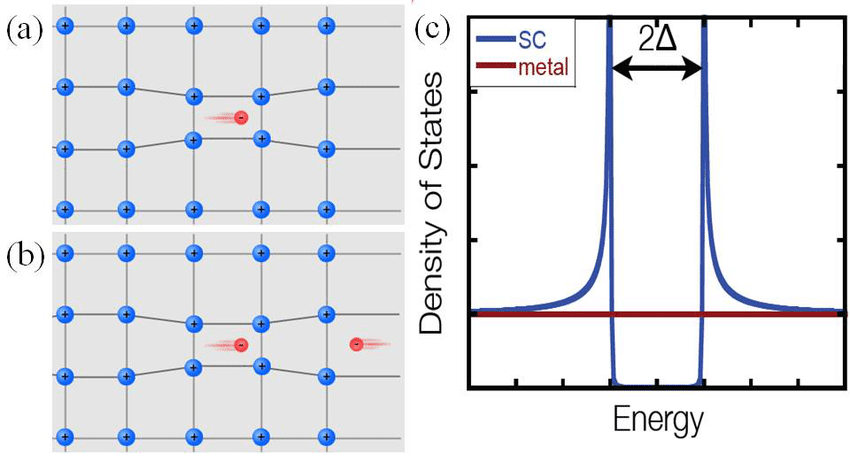
But in a superconductor, there are two electrons that pair together — forming what’s known as a Cooper pair (after Nobel Laureate Leon Cooper) of electrons — that travel together through the band of energy states. The defining characteristic of whether a particle, fundamental or composite, behaves as a fermion or a boson is simply its quantum spin. Electrons are fundamentally spin ½ particles, meaning that they can either be spin “up” (+½) or spin “down” (-½) relative to anything else.

Conventionally, because it’s a fermion (with half-integer spin), if you have one electron in a quantum state that’s spin +½, you can only put one more electron in that state, and it must be spin -½, and then you’re done: no more electrons can occupy that state.

But if you have two electrons under just the right circumstances, one that’s spin +½ and one that’s spin -½, they can pair up to make these Cooper pairs, and then each Cooper pair of electrons together, because (+½) + (-½) = 0, will behave as a boson, or a particle with integer spin. (And 0 is an integer.) As long as these electrons remain bound together in this Cooper pair configuration, they can have the same exact momentum as one another, enabling them to move together in this band, “invisible” to any other set of Cooper pairs that are present.

This figure shows the development and discovery of superconductors and their critical temperatures over time. The different colors represent different types of materials: BCS (dark green circle), Heavy-fermions-based (light green star), Cuprate (blue diamond), Buckminsterfullerene-based (purple inverted triangle), Carbon-allotrope (red triangle), and Iron-pnictogen-based (orange square). The novel states of matter achieved at high pressures have led to the current records, although recent dubious studies have been omitted.

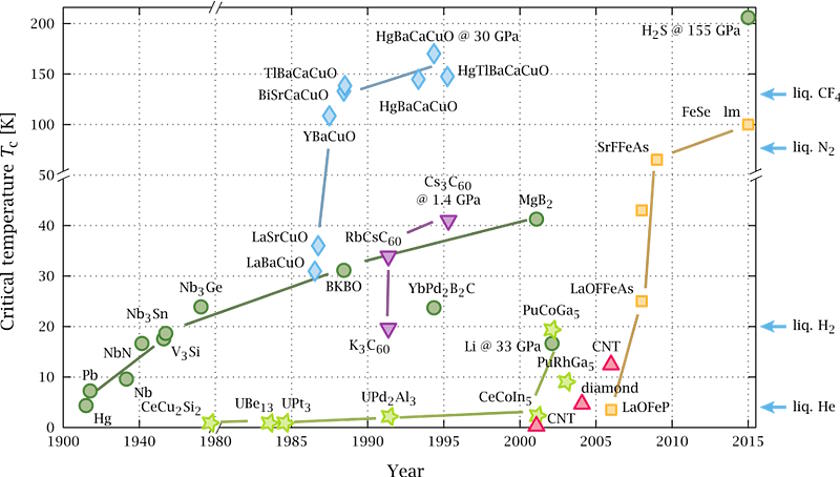
The big problem with making a state like this is the combination of:

• having all the lower-energy states in your material be 100% occupied,
• having the energy levels of the material be such that there’s an unoccupied “band” of energy states just above them,
• and then coaxing the electrons to fall into and remain in a configuration — and keep in mind, this is a delicate configuration — where they’ll pair up into Cooper pairs so that they’ll behave like bosons within that band,

in order to achieve a superconducting state.

This is the reason why nearly all superconducting materials only superconduct at extremely low, near-absolute-zero temperatures: the electrons in the solid material must spontaneously develop that critical energy gap in their spectrum, and then that gap must be filled not by individual electrons, but by pairs of electrons that form and remain in these Cooper pair states. Electrons cannot “jump up” from the filled energy levels from below, and they must not be too energetic so that they pop up out of this band into the higher-energy excited states above it. The hotter your system is, the more particles there are that will spontaneously have enough energy to cause one of those two conditions to be violated, bringing an end to your superconducting state.

This diagram shows the lattice structure of the material known as LK-99: a candidate for a room temperature superconductor. The copper-doped lead-apatite can be easily constructed, but early attempts at demonstrating superconductivity and quantum levitation appear dubious. It may exhibit behavior more akin to a metal-insulator transition than a conductor-superconductor transition, and permanent magnetism, induced by electron-electron interactions, is likely to be an instability that swamps any potential superconductivity.

In the case of LK-99, part of the reason for (justified) theoretical excitement was the calculations showing that, at room temperature and ambient pressure, there would be a “band” of energy states that was nearly continuous, that electrons could occupy under the right conditions.

But would those electrons pair up into these Cooper pairs and remain in that state, providing evidence for superconductivity? Or would those electrons simply behave as normal electrons when they entered that state, behaving like a conventional conductor rather than a superconductor? Looking at the original papers by Lee and Kim (the “L” and “K” in LK-99) themselves, the evidence seems to indicate the former.

The way this plays out — in the mind of a physicist, at least — is to treat materials as though they’re made up of two items: electrons, and the background, ion-containing lattice of the underlying matter. There needs to be an energy gap in the spectrum of electrons within that matter, and the gap has to be larger than the kinetic energy (or the energy of motion) that each individual electron possesses. Keep your electrons and the system they’re in at low energies and low temperatures, and it’s easier to get the electrons to fall into and remain in that gap; the higher the temperature, the greater the kinetic energy, and the more difficult it is to get the electrons to fall into and remain in that gap.

This shows the phase diagram of a hole-doped cuprate superconductor, specifically Bi2Sr2CaCu2O8+δ. The dependence of the superconductivity state on both temperature and the amount of doping (more doping to the right, less doping to the left) can be seen from the diagram. Antiferromagnetic behavior and charge density wave behavior are two electron-electron interactions that can swamp and destroy any superconductivity effects.

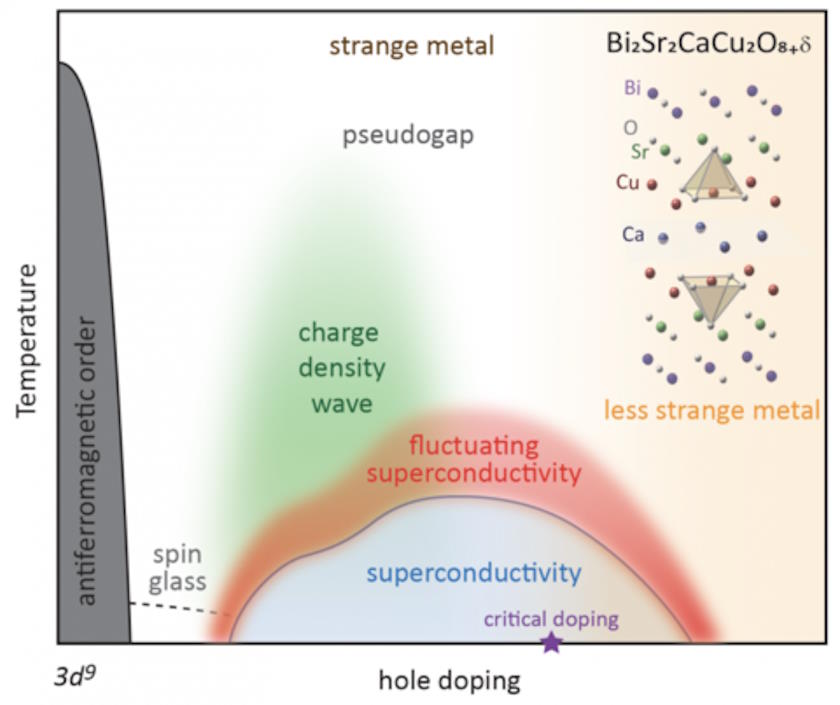
At lower temperatures and energies, there are fewer instabilities that interactions can lead to. Why? Because there are fewer interactions and the interactions that are there are weaker, both between electrons and other electrons and also between electrons and the underlying lattice, than there are at higher temperatures and energies. (If you’ve ever seen the word “phonon” used before, interactions between electrons and that lattice are usually called electron-phonon interactions.)

What happens when electrons interact with other electrons? They can induce instabilities, including:

• density waves (both spin density and charge density waves),
• crystallization effects,
• and permanent, ordered magnetization effects (both ferromagnetism and antiferromagnetism).

Similarly, when electron-phonon interactions occur, they can induce their own instabilities, which typically result in structural instabilities within the material itself: changes in shape, density, volume, etc. Most of these changes destroy the critical, underlying lattice structure that you need to have the energy bands necessary for a superconductor. At higher temperatures, all of these instabilities are more likely to “win out” over the instability that would otherwise lead to a superconducting state.

In a very strong and robust reproduction attempt of Lee & Kim’s LK-99 work, scientists Kaizhen Guo, Yuan Li, and Shuang Jia synthesizes several samples of LK-99 and found no evidence for superconductivity, but instead evidence for what’s known as soft ferromagnetism. Their supplemental figures, with the “partial levitation” (i.e., permanent magnet) effects shown at left and a classical explanation using standard magnetism shown at right.

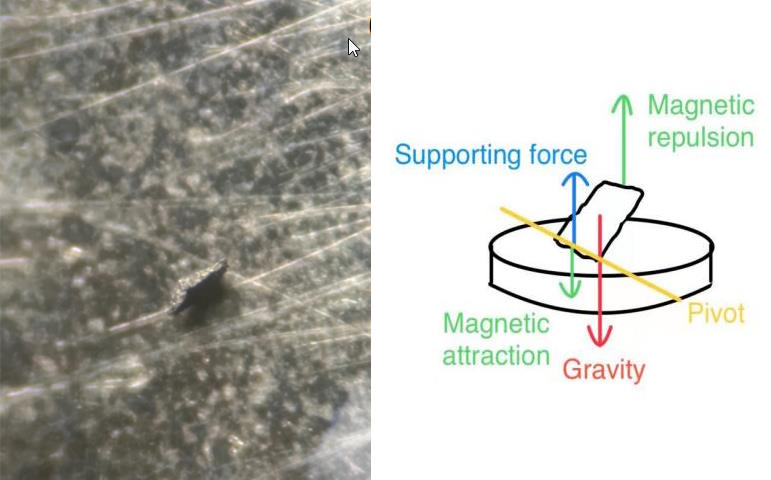
Coming once again back to LK-99, it’s pretty clear that what the original teams were claiming was a quantum levitation effect due to the Meissner effect was not that at all, but was rather the far more common (especially at high temperatures) effect of permanent magnetization. A superconducting state isn’t just because you have the proper conditions in place for it to occur within your material, it’s because you have the proper conditions for it to occur while, simultaneously, no other energetically-induced instabilities occur. If they do, chances are that they’ll supersede/swamp any effects that would otherwise lead to superconductivity.

None of this necessarily means that a high-temperature superconductor is impossible, and this perspective can perhaps help people understand why the current temperature record for superconductors occurs under very high pressures: those high pressures stabilize the lattice, protecting against any underlying changes that would change its structure and, as a result, the band structure of its electron energy levels. But a high-temperature, ambient pressure superconductor? That’s the holy grail of superconductivity for good reason, and having no other instabilities get in its way is why it will truly take a revolutionary material to achieve it.