The Most Important Equation In The Universe

Just one equation relates the expansion of space to all the matter and energy we have. If you know this, you can know the fate of the Universe.
Last week, Perimeter Institute ran a feature where they asked 14 scientists what their favorite equation was, and why. There were many great answers from many different areas of research, from thermodynamics to pure mathematics. Many people went with fundamental equations, like the law of gravity, Newton’s famous F = ma, or the Schrödinger equation, which governs quantum particles. I had the honor of being included in this list, and the answer I gave was none of these. Instead, the equation I picked was a very specific one: the first Friedmann equation, which is derived from Einstein’s General Relativity under a specific set of circumstances.

When they asked why I picked that equation, here’s what I said:
“The first Friedmann equation describes how, based on what is in the universe, its expansion rate will change over time. If you want to know where the Universe came from and where it’s headed, all you need to measure is how it is expanding today and what is in it. This equation allows you to predict the rest!”
The story of Friedmann, his equation, and what it teaches us about our Universe is a story that every science enthusiast should know.

In 1915, Einstein put forth his theory of General Relativity, which related the curvature of spacetime on one hand to the presence of matter and energy in the Universe on the other. As John Wheeler put it many years later, spacetime tells matter how to move; matter tells spacetime how to curve. Einstein’s theory, in one fell swoop, reproduced all the previous successes of Newton’s gravity, explained the intricacies of Mercury’s orbit (which Newton’s theory couldn’t), and made a new prediction for the bending of starlight, which was spectacularly confirmed during the total solar eclipse of 1919. The only problem? In order to prevent the Universe from collapsing in on itself, Einstein needed to add a cosmological constant — an ad hoc fix for the fact that static spacetimes were unstable in General Relativity — to his theory. It was ugly, it was finely-tuned, and it had no other motivation.

Enter Friedmann. In 1922, just three years after the eclipse confirmation, Friedmann found an elegant way to save the Universe while simultaneously doing away with the cosmological constant: don’t assume that it’s static. Instead, Friedmann argued, assume that it is as we observe it, full of matter and radiation, and allowed to be curved. Assume, further, that it’s roughly isotropic and homogeneous, which are mathematical words meaning “the same in all directions” and “the same at all locations.” If you make these assumptions, two equations pop out: the Friedmann equations. They tell you that the Universe isn’t static, but rather that it either expands or contracts depending on what the expansion rate and the contents of your Universe are. Best of all, they tell you how the Universe evolves with time, arbitrarily far into the future or past.
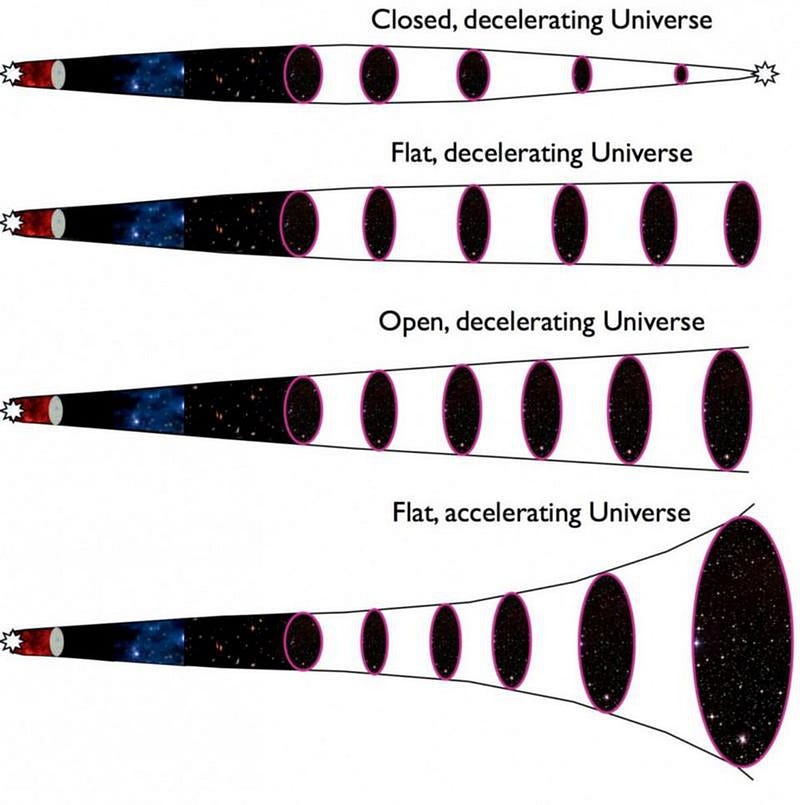
What’s remarkable is that Friedmann put this out before we discovered that the Universe was expanding; before Hubble even discovered that there were galaxies beyond the Milky Way in the Universe! It wouldn’t be until the next year that Hubble would identify Cepheid variable stars in Andromeda, teaching us its distance and placing it far outside of our own galaxy. Furthermore, it wouldn’t be until the late 1920s that Georges Lemaître and later, independently, Hubble, would put the redshift-and-distance figures together to conclude that the Universe was expanding. By that time, the young Friedmann had already tragically died of typhoid fever, which he had contracted while returning from his honeymoon in 1925.

Yet his scientific legacy was indisputable, and became even more so as we came to understand cosmology better. The first Friedmann equation is the most important of the two, since it’s the most easy and straightforward to tie to observations. On one side, you have the equivalent of the expansion rate (squared), or what’s colloquially known as the Hubble constant. (It’s not truly a constant, since it can change as the Universe expands or contracts over time.) It tells you how the fabric of the Universe expands or contracts as a function of time.
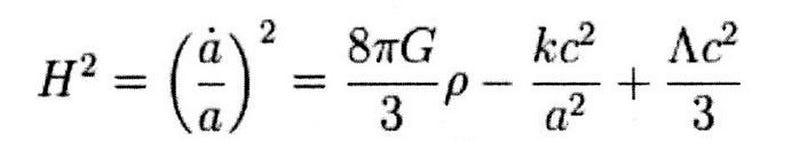
On the other side is literally everything else. There’s all the matter, radiation, and any other forms of energy that make up the Universe. There’s the curvature intrinsic to space itself, dependent on whether the Universe is closed (positively curved), open (negatively curved), or flat (uncurved). And there’s also the “Λ” term: a cosmological constant, which can either be a form of energy or can be an intrinsic property of space.
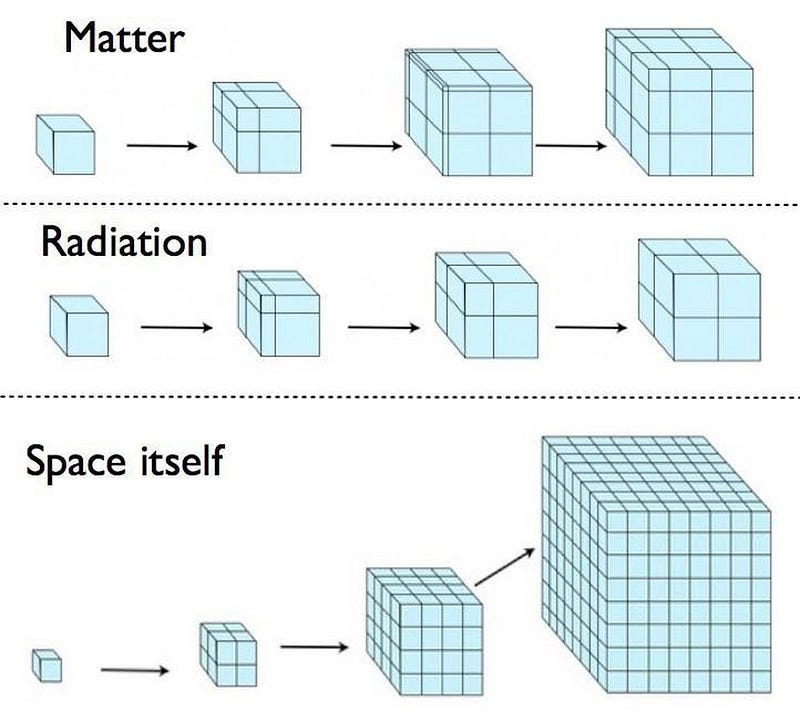
Either way, this is the equation that relates how the Universe expands, quantitatively, to what makes up the matter and energy within it. Measure what’s in your Universe today and how fast it’s expanding today, and you can extrapolate forwards or backwards by arbitrary amounts. You can know how the Universe was expanding in the distant past or immediately after the Big Bang. You can know whether it will recollapse or not (it won’t), or whether the expansion rate will asymptote to zero (it won’t) or remain positive forever (it will).
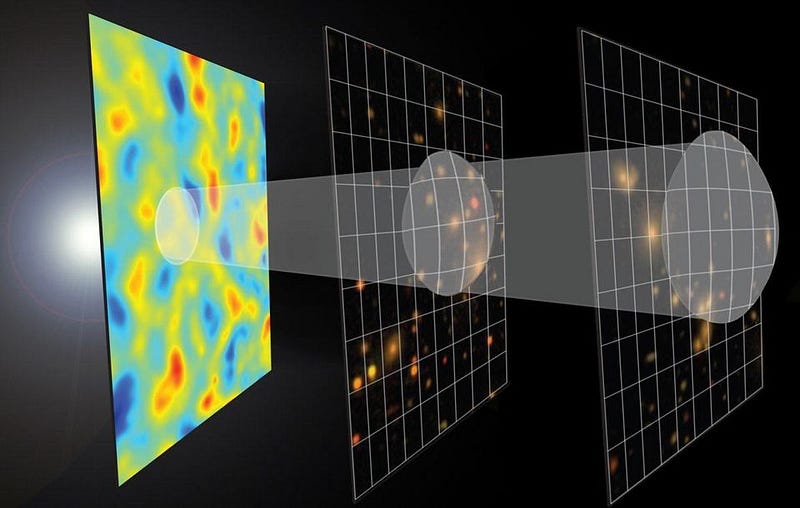
And perhaps most spectacularly, you can add imperfections atop this smooth background. The density imperfections you put into your Universe tell you how large-scale structure grows and forms, what will grow into a galaxy/cluster and what won’t, and what will become gravitationally bound versus what will be driven apart.
All of this can be derived from one single equation: the first Friedmann equation.
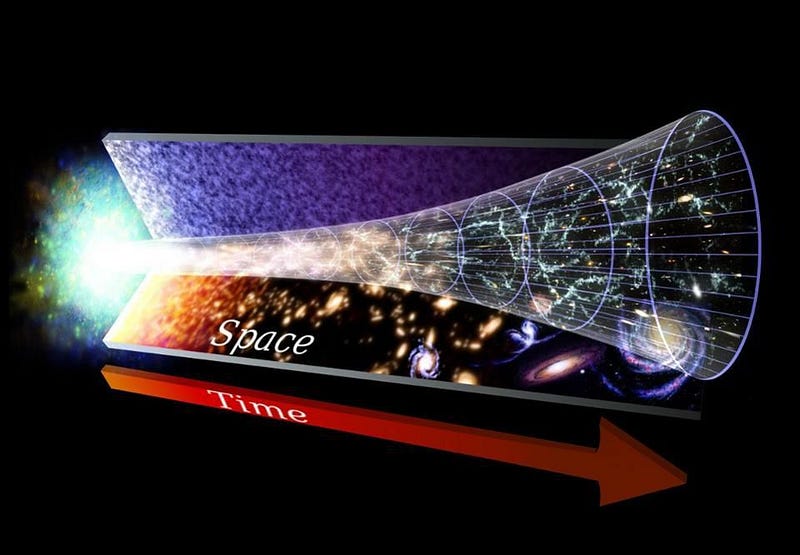
Although Friedmann’s life was short, his influence cannot be overstated. He was the first to derive the General Relativity solution that describes our Universe: an expanding Universe filled with matter. Although it was independently derived, later, by three others — Georges Lemaître, Howard Robertson, and Arthur Walker — Friedmann fully realized its implications and applications, and even came up with the first solutions for exotically curved spaces. He was an influential teacher as well; his most famous pupil was George Gamow, who would later go on to apply Friedmann’s work to the expanding Universe to create the Big Bang Theory of our cosmic origin.
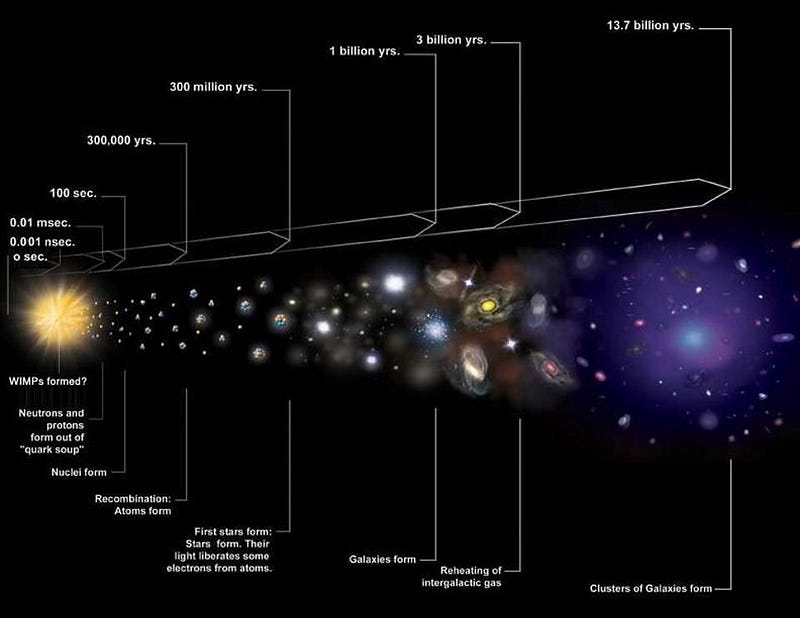
Nearly a century after his most famous work, Friedmann’s equations have been extended to a Universe containing an inflationary origin, dark matter, neutrinos, and dark energy. Yet they’re still perfectly valid, with no additions or modifications required to account for these tremendous advances. While we can all argue about the relative merits of Einstein, Newton, Maxwell, Feynman, Boltzmann, Hawking, and many others, when it comes to the expanding Universe, Friedmann’s first equation is the only one you need. It connects the matter and energy that’s present to the expansion rate today, in the past, and in the future, and allows you to know the fate and history of the Universe from measurements we can make today. As far as the fabric of our Universe is concerned, this equation takes the crown as the single most important.
Ethan Siegel is the author of Beyond the Galaxy and Treknology. You can pre-order his third book, currently in development: the Encyclopaedia Cosmologica.





