No, Scientists Will Never Be Able To Remove The Empty Space From Atoms

It’s absolutely true that atoms are mostly empty space. But removing even that empty space is impossible, and this is why.

If you were to take any object in the Universe that’s made of normal matter ⁠ — anything a human being could touch, see, or otherwise detect an interaction with using our bodies ⁠ — you’d find that you could break it up into smaller and smaller components. An entire human body can be broken up into organs, which in turn are made up of cells. Each cell consists of organelles, which are smaller structures with specialized functions, and the organelles are reliant on interactions that occur at the molecular level.

Composing the full suite of molecules are atoms: the smallest component of normal matter that retains the individual character and properties of the element in question. Elements are defined by the number of protons in each atom’s nucleus, where an atom consists of electrons orbiting that nucleus. But despite the fact that atoms are mostly empty space inside, there’s no way to remove that space. Here’s the story of why.

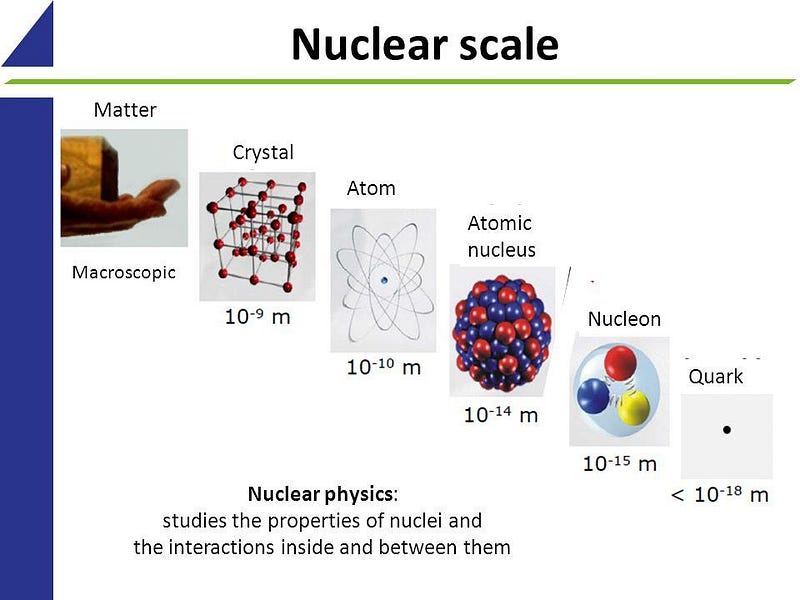
An atom, at the most basic level, consists of a positively charge atomic nucleus that’s extremely tiny in volume. For every proton in the atomic nucleus, there’s an equal and opposite quantum of charge that orbits around it, creating an overall neutral system: the electron.

Yet, whereas the atomic nucleus is confined to an extremely small volume ⁠ — the diameter of a proton is right around 1 femtometer, or 10^-15 m ⁠ — the orbiting electrons, which are themselves point-like particles, occupy a volume that’s approximately 1 ångstrom (10^-10 m) in all three dimensions.

The first experiment that demonstrated this enormous difference is more than a century old, when physicist Ernest Rutherford bombarded a thin sheet of gold foil with radioactive particles.

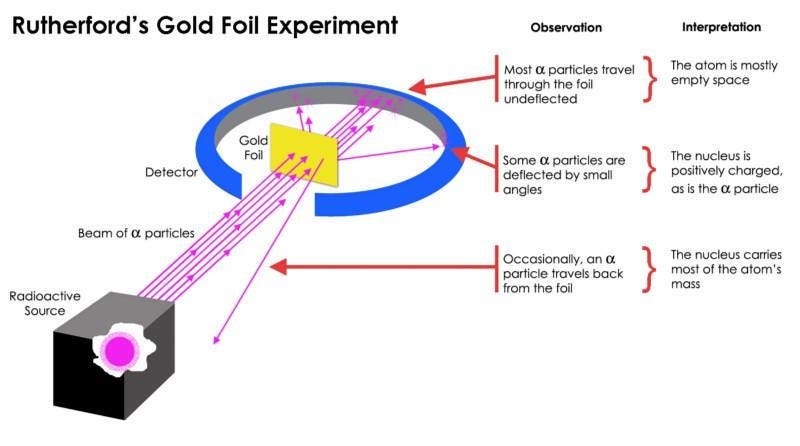
What Rutherford did was simple and straightforward. The experiment began with a ring-shaped apparatus designed to detect particles encountering it from any direction. In the center of the ring, thinly hammered gold foil was placed of a thickness so small it couldn’t be measured with early-20th century tools: likely just a few hundred or thousand atoms across.

Outside of both the ring and the foil, a radioactive source was placed, so that it would bombard the gold foil from one particular direction. The expectation was that the emitted radioactive particles would see the gold foil much the way a charging elephant would see a piece of tissue paper: they’d simply go right through as though the foil weren’t there at all.

But this turned out only to be true for most of the radioactive particles. A few of them — small in number but vitally important — behaved as though they bounced off of something hard and immovable.

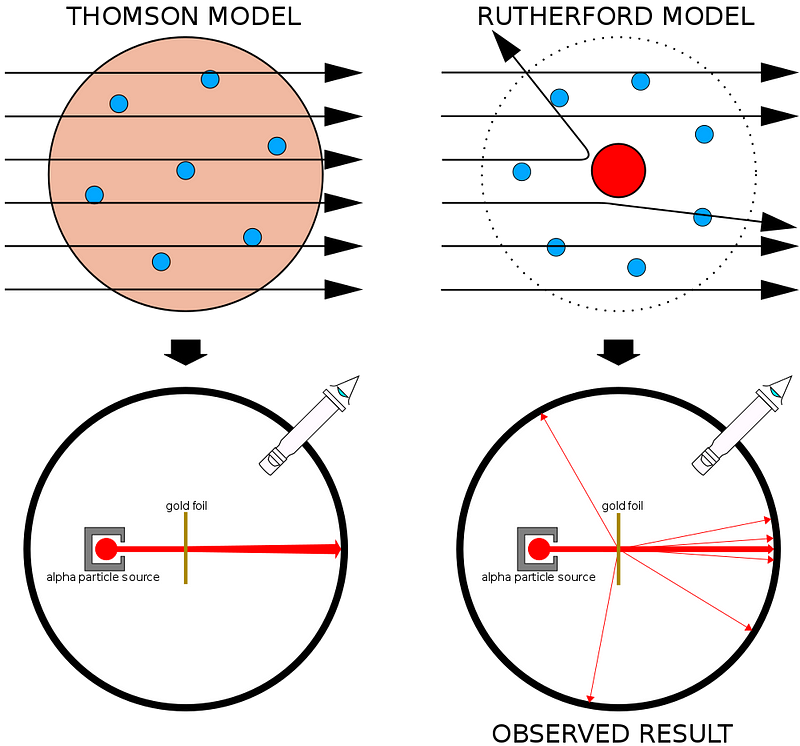
Some of them scattered off to one side or the other, while others appeared to ricochet back towards their direction of origin. This early experiment provided the very first evidence that the inside of an atom wasn’t a solid structure as previously envisioned, but rather consisted of an extremely dense, small core and a much more diffuse outer structure. As Rutherford himself remarked, looking back decades later,

“It was quite the most incredible event that has ever happened to me in my life. It was almost as incredible as if you fired a 15-inch shell at a piece of tissue paper and it came back and hit you.”

This type of experiment, where you fire a low, medium, or high-energy particle at a composite particle, is known as deep inelastic scattering, and it remains our best method for probing the internal structure of any system of particles.

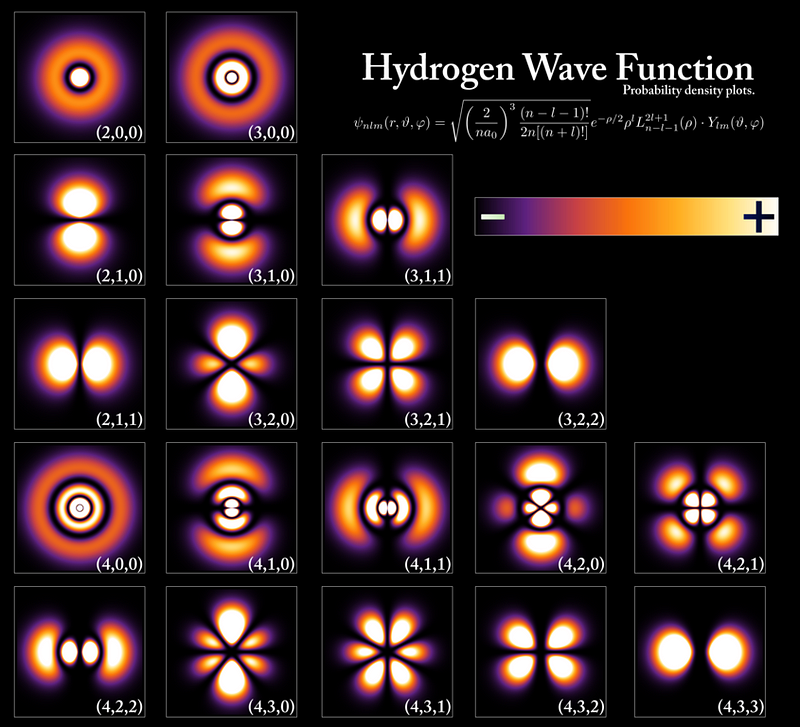
For the atom, from a simple one like hydrogen to a complex one like gold, lead or uranium, the electrons can be found far beyond the extent of the atomic nucleus. Whereas an atomic nucleus is confined to a volume that’s about 1 cubic femtometer (10^-15 meters on each side), an electron can be found distributed probabilistically over a volume that’s approximately a quadrillion (10¹⁵) times larger. This property is independent of which element we consider, the number of electrons present (so long as it’s at least one), or which method we use to measure the electron or the nucleus.

The fact that atoms are mostly empty space is known, today, even to most schoolchildren, who learn this fact at about the same time that they learn about the structure of atoms. Upon learning this, many of them wonder — as I’m sure many of you wonder — why you cannot just remove that empty space and compact atoms down to much smaller scales, like the size of an atomic nucleus?

In the classical world, where nature plays by rules that we’re familiar with and that match up with what our intuition predicts, it’s very easy to control the positions of particles. But at the quantum level, there’s a fundamental limitation set by the rules of nature: the Heisenberg uncertainty principle.

Even if you know everything there is to know about an electron orbiting an atomic nucleus, including:

• what energy level it occupies,
• what its quantum state is,
• and how many other electrons there are in surrounding energy levels,

there will still remain a number of properties that are inherently uncertain. In particular, one of the inherently uncertain properties is the electron’s position; we can only plot out the probability distribution of where the electron is likely to be.

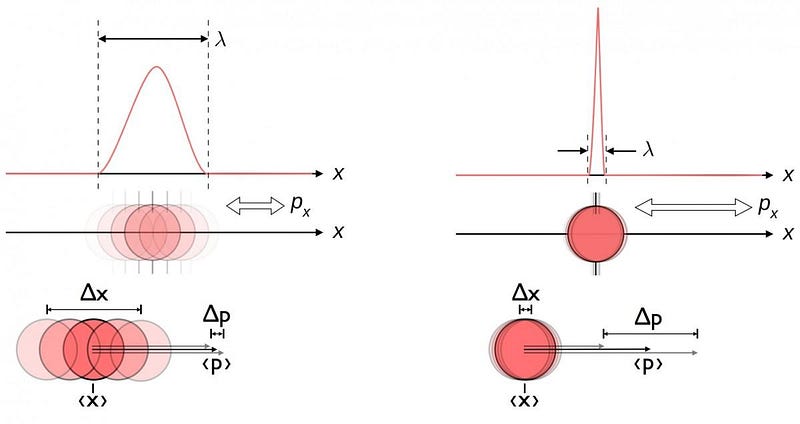
The reason for this is the inherent quantum uncertainty between position and momentum. The momentum of an electron, which we can think about as the unit-of-motion any particle will have, can be known to a certain precision by performing a specific measurement.

However, the more precise your momentum-revealing measurement is, the greater an inherent uncertainty the act of measuring it will impart to the electron’s position. Conversely, the more precisely you attempt to measure the electron’s position, the greater the uncertainty you induce in the electron’s momentum will be. You can only know those two quantities — position and momentum — to a limited precision at the same time, as measuring one more precisely will create an inherently larger uncertainty in the one you don’t measure.

The electron naturally occupies the large volume we’ve come to expect around the atomic nucleus for two reasons.

1. The size of the probability cloud that the electron occupies is dependent on the charge-to-mass ratio of the electron. With the same magnitude charge as the proton but just 1/1836th the mass, even the ultra-strong electromagnetic force cannot confine the electron to a smaller volume than we see.
2. The outward force compressing an electron down onto an atomic nucleus, restricting the outer components of the probability cloud, is extremely small even for atoms bound together in an ultra-strong lattice. The forces between the electrons in two different atoms, even in atoms that are bound together, is very small compared to the force between the atomic nucleus and an electron.

Each of these reasons gives us a hope for a workaround that works in practice, but with limited applicability.

You can replace the electron with a more massive particle with the same electric charge. There are two electron-like particles that exist in the Standard Model with the same charge as the electron: the muon and the tau. The muon is about 200 times as massive as an electron, and so an atom of muonic hydrogen (with a proton for a nucleus but a muon instead of an electron orbiting it) is about 200 times smaller than standard hydrogen.

If you bind muonic hydrogen to a number of other atoms, they will serve as a catalyst for nuclear fusion, allowing it to proceed with much lower temperatures and energies than standard fusion. However, muons only live for ~2 microseconds before decaying away, and the more massive tau lives for less than a picosecond. These exotic atoms are too transient to remain useful for long.

Alternatively, you can increase the pressure on the atoms enormously by piling up incredible amounts of mass in one single location in space. An individual atom in isolation might be just an ångstrom in size, but if you pile a star’s worth of material around it, that atom will feel an outside pressure that “squeezes” the electron to occupy a much more confined volume.

The greater the pressure, the more confined the electrons are, and the smaller the atoms are in terms of physical extent. There’s a limit to the outside pressure the atoms can withstand before the same catastrophe as earlier occurs: the atomic nuclei get so close together that their wavefunctions overlap and nuclear fusion can occur. In a white dwarf, this threshold occurs at about 1.4 solar masses; exceed it, and you’ll wind up initiating a runaway fusion reaction, which results in this case in a type Ia supernova.

It might be a delightful science fiction dream to remove the empty space from atoms, decreasing the volume that matter occupies by factors of millions, trillions or even more. However, it isn’t that the electrons orbiting the nucleus inherently occupy an extremely large volume of space, but rather that the quantum properties inherent to particles — masses, charges, interaction strength, and quantum uncertainty — all combine to create the atoms that exist in our Universe.

Even if we had a stable, heavier counterpart of the electron, or the ability to compress matter to arbitrarily dense states, we’d run into a quantum threshold where the atomic nuclei at the centers of atoms would spontaneously fuse, preventing stable configurations of multiple atoms from existing at all. The fact that our atoms are mostly empty space permits the existence of molecules, chemistry, and life.

Removing the empty space from atoms might be a fun thought experiment, but atoms are the size they are because of the rules of the Universe. Our existence is dependent on that empty space being present, but with the constants of nature having the values they do, don’t worry. It cannot be any other way.