No, There Isn’t A Black Hole At The Center Of The Earth

Even in the most exotic scenario imaginable, they still can’t remain stable in the Earth’s interior.
It’s well known among scientists that if you submit even the most nonsensical paper to enough journals, it will eventually sneak past a lazy peer reviewer and get published. Recently, a word-salad-esque paper — obviously a fake study — claimed that a black hole at the center of the Earth is responsible for all sorts of questionable and suspicious phenomena. The big story that people are latching onto is one of predatory open access journals and the pitfalls of sham peer review, which certainly is a widespread problem in the modern world of scientific publishing.
But there’s a fascinating opportunity here as well: to expose the real science behind why someone would be interested in the notion that the center of the Earth could contain a black hole. It’s a wild idea that isn’t necessarily based in nonsense, but the data we’ve collected has thoroughly demonstrated that there isn’t a black hole at the center of the Earth. Here’s the story of how we scientifically know that the Earth’s interior is black hole-free.

The Universe we have, to the best of our knowledge, is governed by two fundamental sets of rules: General Relativity, which tells us how matter and energy are related to the fabric of spacetime and how the gravitational force works, and Quantum Field Theory, which tells us how the various particles interact with one another via the electromagnetic and nuclear forces.
One place where these two theories come together is in the science of black holes: where so much mass exists in such a small region of space that quantum effects can become important. This scenario — where spacetime is significantly curved but effects that occur on quantum scales have physically meaningful consequences — provides us with a regime to test the limits of what’s presently known about the Universe. In theory, black holes are the perfect natural laboratory to look for effects that could take us beyond what we presently know about the Universe.

General Relativity and Quantum Field Theory calculations are both normally conducted in four dimensions: three space dimensions and one time dimension. Forces get weaker as you move away from the source that creates them — mass/energy for gravitation, charges for the other forces — as the effects that they have spread out over all the space available to them. In three spatial dimensions, we’ve worked out precisely how an enormous suite of physical systems will behave.
One of those systems is for black holes. Black holes are what you form when you get so much matter/energy together in one location that an event horizon forms: a region of space that’s so severely curved that nothing in the Universe, not even light, can escape from within it. Black holes, because the curved space around them has different properties when compared to the flatter space farther away from them, always spontaneously radiate energy away by their very nature. This released energy, known as Hawking radiation, comes at the expense of the mass of the black hole.

This means, over time, that black holes will evaporate, with the lowest-mass black holes evaporating the most quickly. Like everything in the Universe, however, there are limits. If you make your black hole too small — i.e., too low in mass — then the amount of time it will take to evaporate becomes shorter than the Planck time: the timescale on which physical measurements and the predictions of our theories are meaningful.
Remember, in the quantum Universe, there’s a fundamental uncertainty to certain pairs of quantities: angular momentum in two perpendicular directions, momentum and position, or energy and time. The shorter the timescale you’re attempting to describe, the larger the uncertainty in your energy is. If you go below the Planck time, which corresponds to ~10^-43 seconds, the size of your quantum fluctuations are going to be larger and more massive than the mass of a black hole that would evaporate on that short timescale.
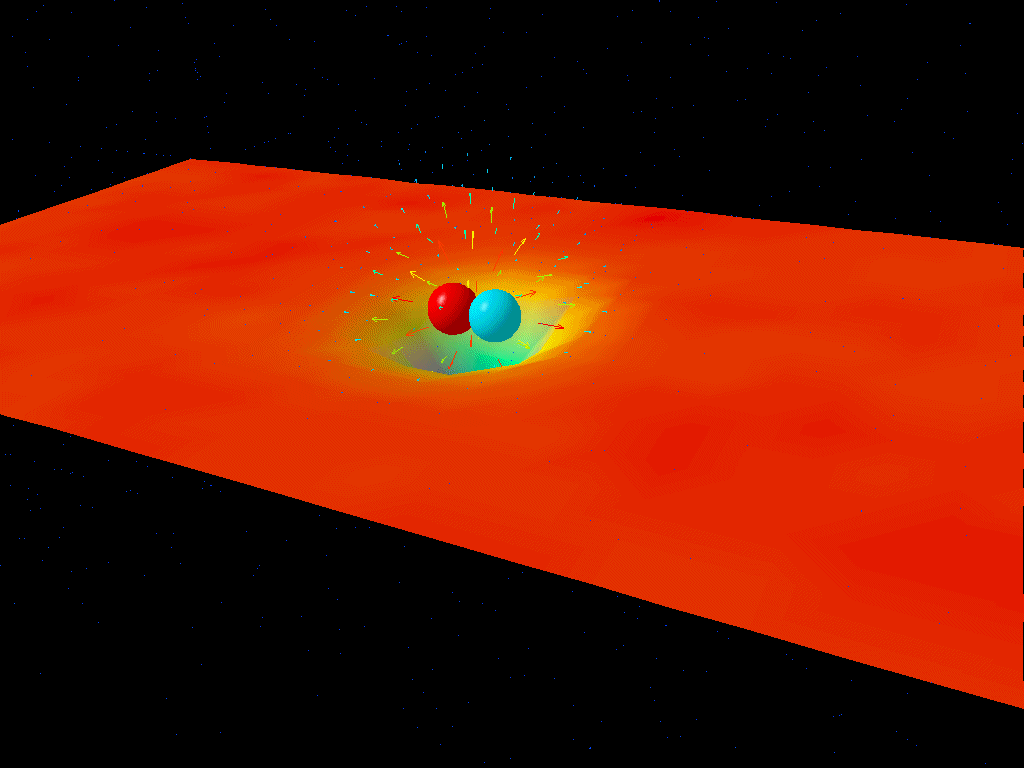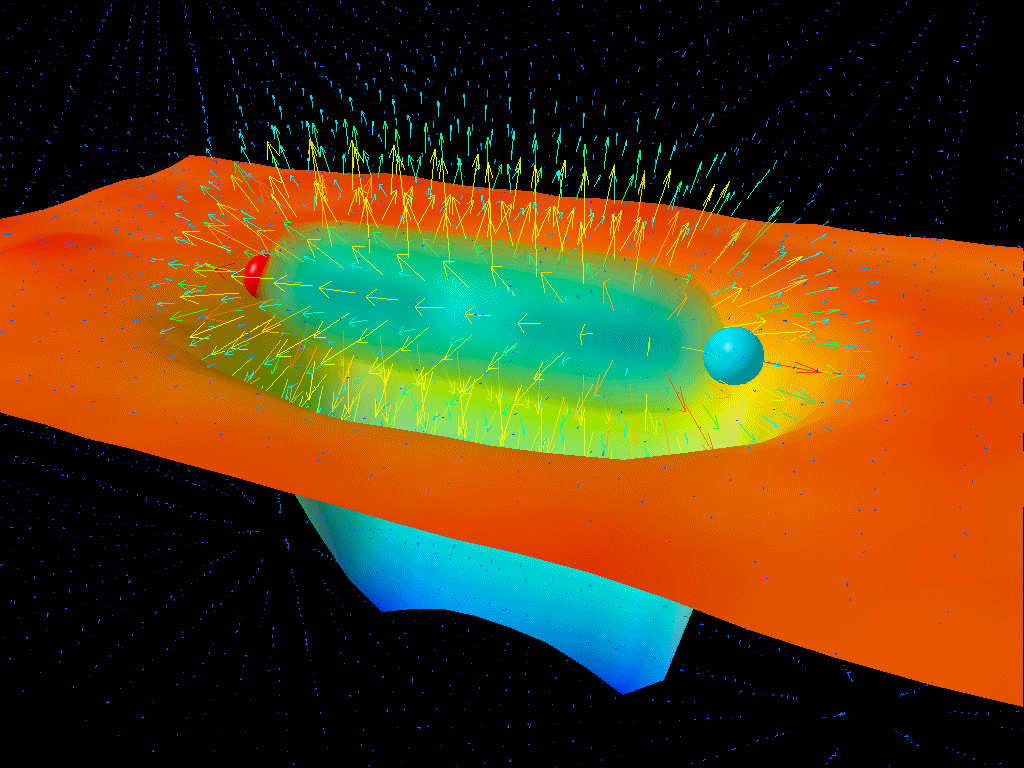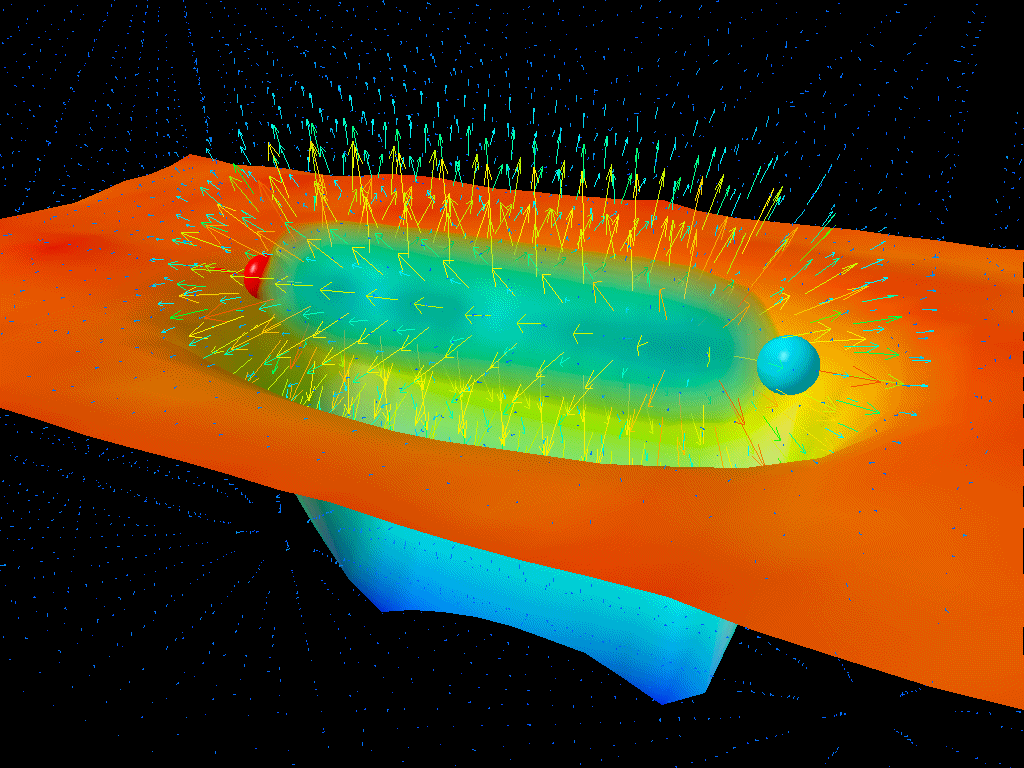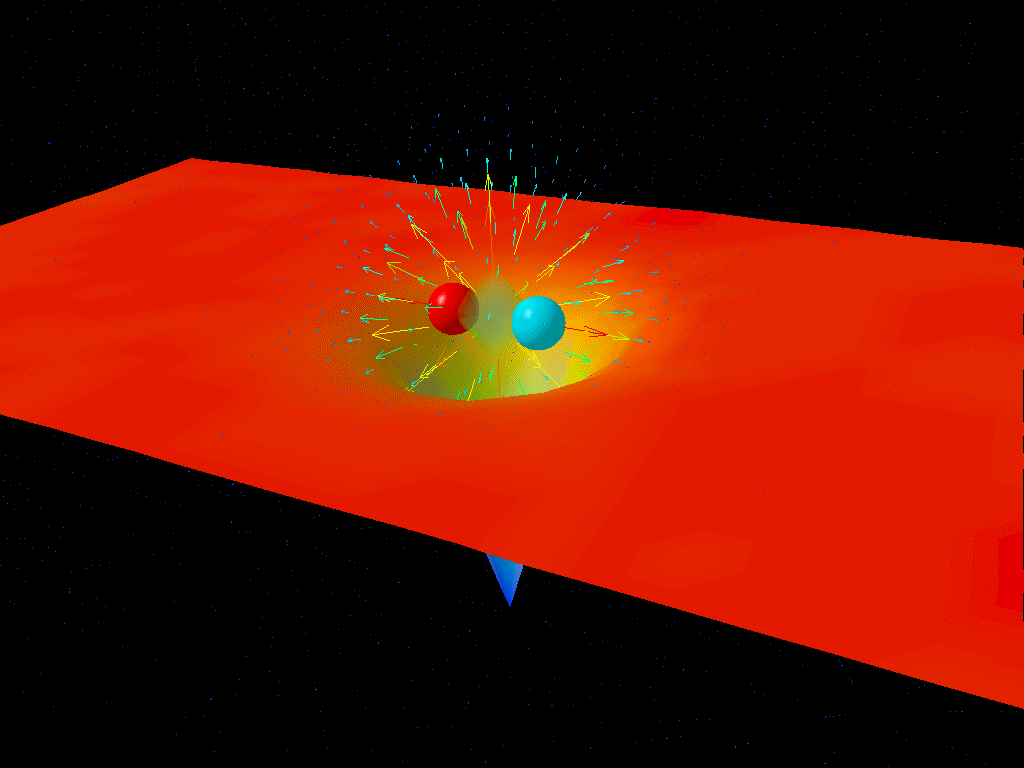
For this reason, there’s a minimum timescale, a minimum length scale, and a minimum black hole mass for which physics makes sense. The energies required to create a black hole that’s larger than this minimum mass aren’t huge by our macroscopic standards: about 22 micrograms, or the energy you release from burning roughly one standard automobile’s gas tank (14 gallons / 53 liters) of crude oil. That’s not a lot of energy spread out over a system of many particles, but for a single particle, that represents an energy of ~10²⁸ eV (electron-volts), or about a quadrillion times the energy of what the LHC, the world’s most powerful particle accelerator, can achieve.
At least, this is how physics works if there are exactly three dimensions of space.
But if there are more dimensions of space, and those dimensions are large compared to that theoretical minimum length scale, then gravity can spread out into not only our three known spatial dimensions, but these additional dimensions as well. If these “large extra dimensions” exist, then there are theoretical scenarios where black holes of significantly lower energies (and masses) than these expected limits can exist, and those same extra dimensions can prevent them from immediately decaying away.

Of course, we can calculate what happens in these scenarios, and the picture we arrive at isn’t exactly rosy for these black holes. Even if they could exist — which is to say, if cosmic rays and/or the LHC could create them — their mass would be tiny. Not on the order of micrograms, but of a tiny, tiny fraction of a gram: about 10^-23 kg, or the equivalent of about 10,000 protons all combined together.
If we had only our standard three spatial dimensions, the black hole would decay after only 10^-83 seconds, which is some 40 orders of magnitude too short to actually exist in our Universe. But if we have a fourth spatial dimension, and that dimension is “large” compared to that minimum length scale, the decay time can rise all the way up to 10^-23 seconds: long enough to exist.
But, is existing for this incredibly short timescale enough? Let’s look at what this black hole would need, even in the presence of a large extra dimension, to survive.

Because of the ultra-short decay timescale, the only way the black hole could survive is in the following two ways:
- either you need to add some new physics to keep black holes from decaying away altogether,
- or you need to find some way for these black holes to consume enough mass rapidly enough that they grow faster than they decay.
The first option can’t be ruled out, but it shouldn’t be seriously considered. In theoretical physics, there’s a general rule that’s never been codified, but that everyone agrees with, and it’s this: “you’re only allowed to invoke God once.”
What that means is that we already made a wild theoretical leap to assume the existence of not only an extra spatial dimension, but an extra spatial dimension that’s large compared to the minimum length scale. If we need to then take another wild theoretical leap in order to have these tiny black holes be stable, that’s a bridge too far; we’re no longer within the realm of reasonable scientific speculation.

But the latter option is a real possibility. If we create a tiny black hole such as this on Earth, and the black hole then passes into (or through) the Earth, you can envision a scenario where:
- you have a small-mass, small-size black hole moving rapidly through the Earth,
- and yes, it’s evaporating and losing mass, but it’s simultaneously colliding with particles and devouring them, gaining mass,
- and that if it can move fast enough and encounter enough particles, it can gain mass fast enough to grow,
- and that as it gains mass, it sinks to Earth’s center, where it remains, continuing to grow as new particles encounter it, until the entire Earth is catastrophically consumed.
It’s that intermediate step that will be critical, though, to determining whether this is feasible: can the black hole devour matter faster than it radiates energy away and decays?
Fortunately, this is a calculation we can perform.

In the brief time a low-mass black hole like this can live — even assuming we have that extra, large spatial dimension we’re hoping for — it would need to encounter and devour 10,000+ protons-and-neutrons in order to survive, growing faster than it decays. But that means encountering a nuclear particle every ~10^-27 seconds or less, which is very difficult for the following reason:
- the typical distances between atomic nuclei in a solid is 1 ångström: 10^-10 meters,
- a black hole moving at the speed of light, the speed limit of the Universe, can only travel a few billionths of that distance in the necessary time,
- unless it’s moving so quickly that time dilates for it by a factor of many hundreds of millions, requiring it to travel at ~99.9999999999999999% the speed of light.
Unfortunately, even if you created a low-mass black hole with those properties, even if the fourth dimension existed, and even if it headed into the Earth moving at that incredible speed, it would drop below that speed the very instant it swallowed its first nuclear particle. The change in momentum simply from devouring a single proton, like any inelastic collison, would cause the decay rate to rise to unacceptably large values compared to the growth rat. In well under a nanosecond, such a black hole would completely evaporate.

Even under the most optimistic, realistic scenario, there can be no black holes that survive for more than a fraction-of-a-second inside the Earth. If we only have three spatial dimensions, the particles that exist — whether in terrestrial particle accelerators or from the natural cosmic accelerators found in space — can never create a black hole here on Earth. But if there’s a fourth spatial dimension, they can theoretically be created, although the LHC has been unsuccessful in creating and detecting them thus far.
Even in that exotic scenario, however, the laws of physics very definitively prohibit them from remaining stable, as they will decay away. Even if you contrive a scenario to maximize their growth rate, it’s extraordinarily unsustainable, as the growth rate will drop below the decay rate in short order, causing them to evaporate completely. We know enough science to robustly conclude that there isn’t a black hole at the center of the Earth, and any scientist or layperson can follow these same steps to figure out that same conclusion for themselves.
Starts With A Bang is written by Ethan Siegel, Ph.D., author of Beyond The Galaxy, and Treknology: The Science of Star Trek from Tricorders to Warp Drive.