Ask Ethan: How do gravitational waves escape from a black hole?

They move at the speed of light, but not even light can escape. So how do gravitational waves?
“I think there are a number of experiments that are thinking about how you could look in different frequency bands, and get a glimpse of the primordial gravitational wave background. I think that would be really revolutionary, because that would be your first glimpse at the very first instant of our Universe.” –Dave Reitze, LIGO’s executive director
Perhaps the greatest discovery of all announced in 2016 was the direct detection of gravitational waves. Even though they had been predicted by Einstein’s general theory of relativity 101 years prior, it took the development of a laser interferometer sensitive to ripples in space that would displace two mirrors separated by multiple kilometers by less than 10^-19 meters, or 1/10,000th the width of a proton. This finally came to pass during LIGO’s 2015 data run, and two bona fide black hole-black hole merger events unambiguously popped out of the data. But how does physics actually allow this? Mārtiņš Kalvāns wants to know:
This question has puzzled me for a long time. Articles about LIGO discovery state that some percentage of black hole merger mass was radiated away, leaving [a] resulting black hole smaller than [the] sum of [the] original mergers. Yet it is accepted that nothing escapes black holes […] So my question is: how was energy radiated from black hole mergers?
This is a really deep question, and goes straight to the heart of black hole physics and general relativity.

On the one hand, we have a black hole. All of its mass/energy is concentrated together at a singularity at the center, and it’s forever invisible to the outside observer thanks to the presence of an event horizon. Inside a certain region of space (defined by the event horizon), any path that any particle can take, whether massive or massless, regardless of speed or energy, will inevitably take it into the black hole’s central singularity. This means that any particle that enters the event horizon, crosses into the event horizon or otherwise ever finds itself inside the event horizon will never be able to get out, and thus its energy is trapped inside forever. Once you’re inside a black hole, you simply become part of the singularity’s properties: mass, charge (of all different types), and spin. That’s it.

On the other hand, Einstein’s general relativity tells us that when two masses (of any type) orbit one another, it creates ripples in the fabric of space itself as the orbits themselves decay. These ripples, known as gravitational waves, move at the speed of light, cause space to expands-and-contract whenever they pass through it, and carry energy. Because of Einstein’s most famous equation, E = mc2 (or, as he wrote it originally, m = E/c2), we know that one source of energy is mass and one source of mass is energy. They can be converted into one another; mass is only one particular form that energy can take on.

So when LIGO released the results of the event that occurred on September 14, 2015 in January of this year, it was only mildly surprising that they found two black holes — of 36 and 29 solar masses — merging together to create a new black hole of 62 solar masses. Where did the other 3 solar masses (about 5% of the total system’s mass) go? In the energy of gravitational waves. With subsequent events that have been detected, roughly the same trend emerges: two black holes of comparable masses inspiral and merge together, and up to around 5% of their total initial masses gets radiated away in the form of gravitational waves.
But each black hole has an event horizon. Each of the pairs has one before the merger, the final post-merger black hole has one, and at no point during the merger does either singularity become “naked” or ever emerge from an event horizon. So, how does the mass get out?
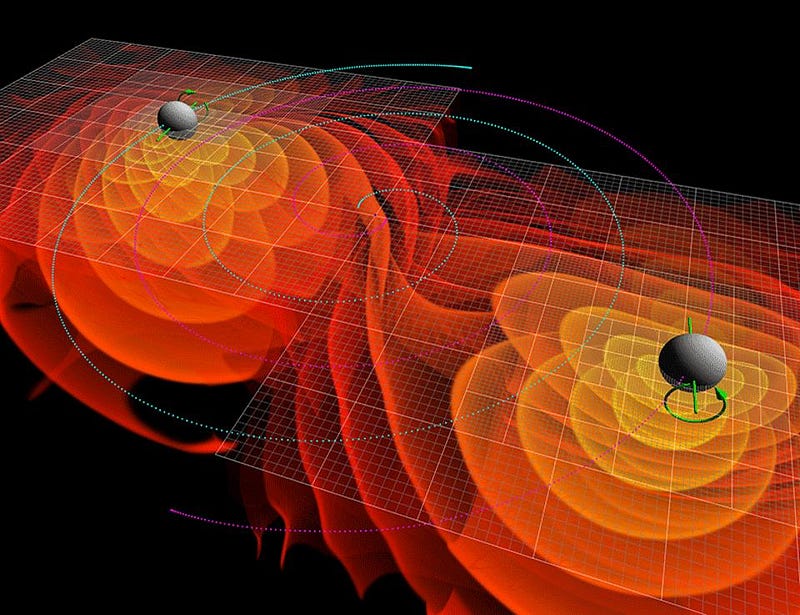
It’s not just a tricky question; it’s a trick question! It’s like asking where the mass goes when protons fuse into deuterium, helium-3 and then helium-4 in the Sun. Why is helium-4 less massive than the four protons that made it up? Because of nuclear binding energy. A bound state is more stable and has less energy (and hence, less mass) than the unbound state. When two black holes inspiral, coalesce and merge, these two black holes are becoming more bound — more gravitationally bound — than they were before. The energy they’re losing is due to gravitational binding energy, not because either of the masses is exiting the event horizon.
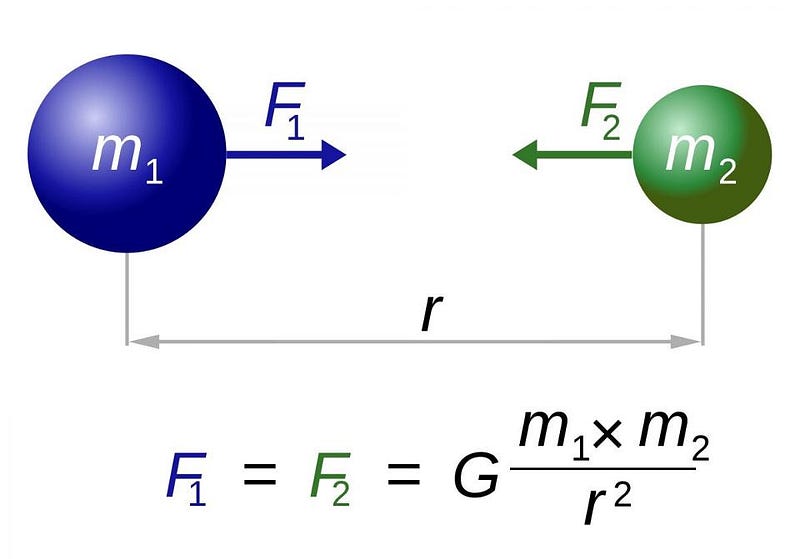
You can see this just from Newtonian gravity. Imagine you have two masses of 1 kg each, each at rest and mutually separated by an infinite distance. They have a certain amount of energy inherent to them in this system: 1.8 × 10¹⁷ Joules, which you can get from Einstein’s equation, E = mc2. Now bring them in to one another, and bring the distance down.
- If they’re now separated by only one kilometer, the whole system has lost 6.67 × 10^-14 Joules of energy.
- If you reduce that separation to one centimeter, the system loses 6.67 × 10^-9 Joules.
- If you bring that separation down to the size of a proton, at 10^-15 meters, the system now loses an incredible 6.67 × 10⁴ Joules, or 66,700 Joules. (Now we’re getting somewhere!)
- And so if you want to lose a really significant amount of energy, you can imagine taking the separation all the way down to 10^-27 meters, where you’ll lose 6.67 × 10¹⁶ Joules, or about 35% of the original energy!

Of course, our Universe obeys general relativity on these scales, not Newtonian gravity, but the picture is the same. It isn’t that the black holes are losing mass; it’s that the total amount of energy in spacetime is transforming from one form — in two well-separated, unbound masses — to another form: a single, tightly bound mass plus gravitational radiation. The orbital properties and the masses of the original black holes determine what percentage of the total original mass becomes binding energy, but in all cases it’s always true that the final mass is larger than either of the original masses but smaller than the combined raw masses. 5% is the amount that’s radiated away in the maximal case, where the two masses are roughly equal. If they had an incredible amount of energy in their spins and their spins were aligned, that percentage can be bumped up all the way to about 11%. But if one of the masses is much greater than the other, the percentage drops; a 1 solar mass black hole merging with a 1,000,000 solar mass one can only radiate away 0.0001% of its energy.

The inspiral and merger doesn’t result in anything from inside the black hole getting out, but rather in spacetime deforming to account for the gravitational potential energy as the two masses coalesce and merge. The ringdown phase — which occurs at the end of the merger — represents the event horizon reverting to its maximally efficient shape: either a sphere or a spheroid. It’s the very last fraction-of-a-second of the merger where the most energy is released, but no particles from inside the black hole are getting out. Einstein’s predictions are very clear, and this is why we were able to make the detections in the first place: because we had calculated what signal to look for. Our intuition may give us trouble, but that’s why we have the equations. Even when our instincts are no good, the calculations will give us the scientific truth.
Submit your Ask Ethan questions to startswithabang at gmail dot com!
This post first appeared at Forbes, and is brought to you ad-free by our Patreon supporters. Comment on our forum, & buy our first book: Beyond The Galaxy!