What was it like when the Higgs gave particles mass?

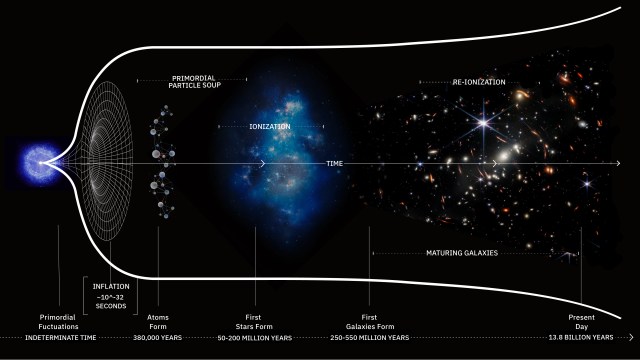
In the earliest stages of the hot Big Bang, the Universe was filled with all the particles, antiparticles, and quanta of radiation it had the energy to create. As the Universe expanded, it cooled: the stretching fabric of space also stretched the wavelengths of all the radiation within it to longer wavelengths, which equates to lower energies.

If there are any particles (and antiparticles) that exist at higher energies that are yet to be discovered, they were likely created in the hot Big Bang, so long two things are true:

• that all necessary quantum conservation laws (spin, energy, charge, angular momentum, etc.) are still obeyed, and
• there was enough energy (E) available to create a particle of that particular mass (m) via Einstein’s E = mc².

It’s possible that a slew of puzzles about our Universe, including the origin of the matter-antimatter asymmetry and the creation of dark matter, will wind up being solved by new, yet undiscovered physics at these early times. But the massive particles we know today would all appear foreign to us under the earliest conditions of the hot Big Bang. At these early stages, none of them have any mass at all.

Any cosmic particle that travels through the Universe, regardless of speed or energy, must contend with the existence of the particles left over from the Big Bang. While we normally focus on the normal matter that exists, made of protons, neutrons, and electrons, they are outnumbered more than a billion-to-one by the remnant photons and neutrinos/antineutrinos. When a charged particle travels through the intergalactic medium, regardless of how it’s produced, it cannot ignore the “bath” of photons it will experience along its journey.

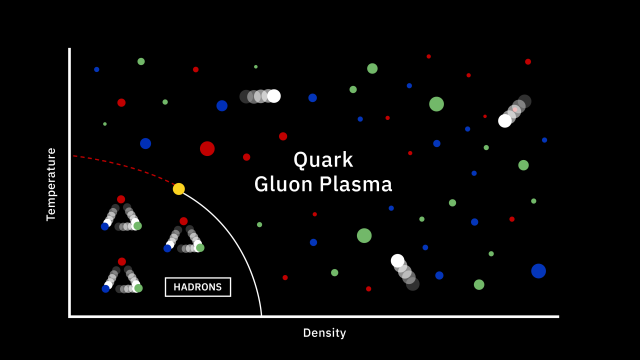
The particles and antiparticles of the Standard Model are easy to create in the early stages of the hot Big Bang, even as the Universe cools and the fractions-of-a-second tick by. The Universe might start off at energies as large as 10¹⁵ or 10¹⁶ GeV; even by the time it’s dropped to 1000 (10³) GeV, there’s still enough energy to easily create each and every Standard Model particle and antiparticle. At the energies achievable by the LHC, we can create the full suite of particle-antiparticle pairs that are known to physics, which includes every species of particle described by the Standard Model.

But at this early point in cosmic history, unlike today, each and every one of them has absolutely no mass at all; they’re entirely massless. If they have no rest mass, they have no choice but to move at the speed of light.

What’s the reason that all quanta find themselves in this strange, bizarre state that’s so different from how they exist today? It’s because the fundamental symmetry that gives rise to the Higgs boson — the electroweak symmetry — has not yet broken in the Universe.

The particles and antiparticles of the Standard Model have now all been directly detected, with the last holdout, the Higgs boson, falling at the LHC earlier this decade. Today, only the gluons and photons are massless; everything else has a non-zero rest mass.

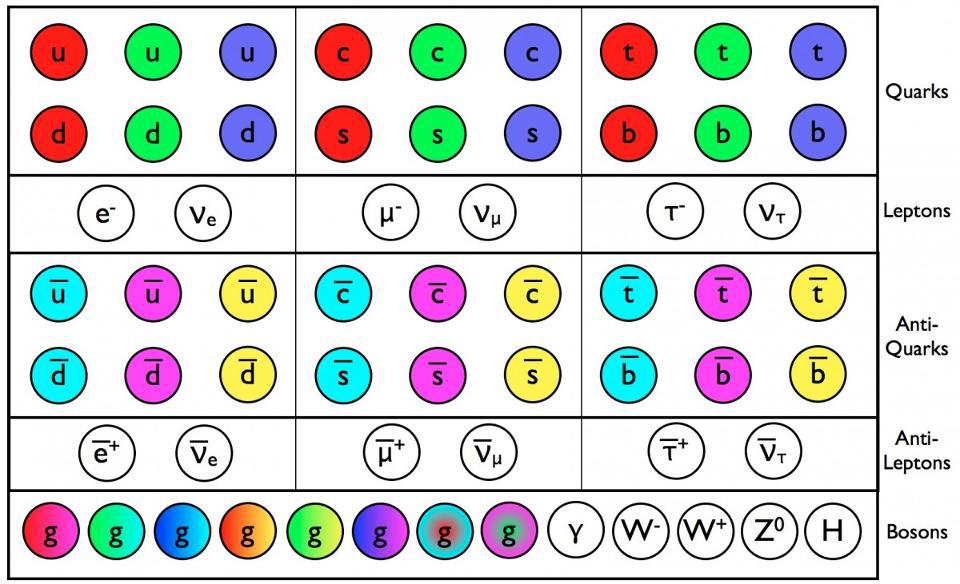
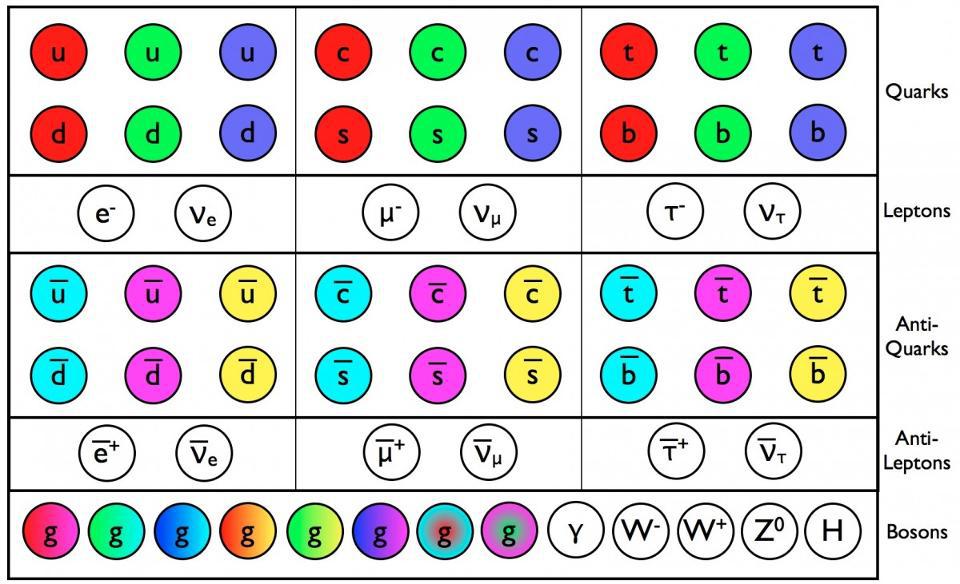
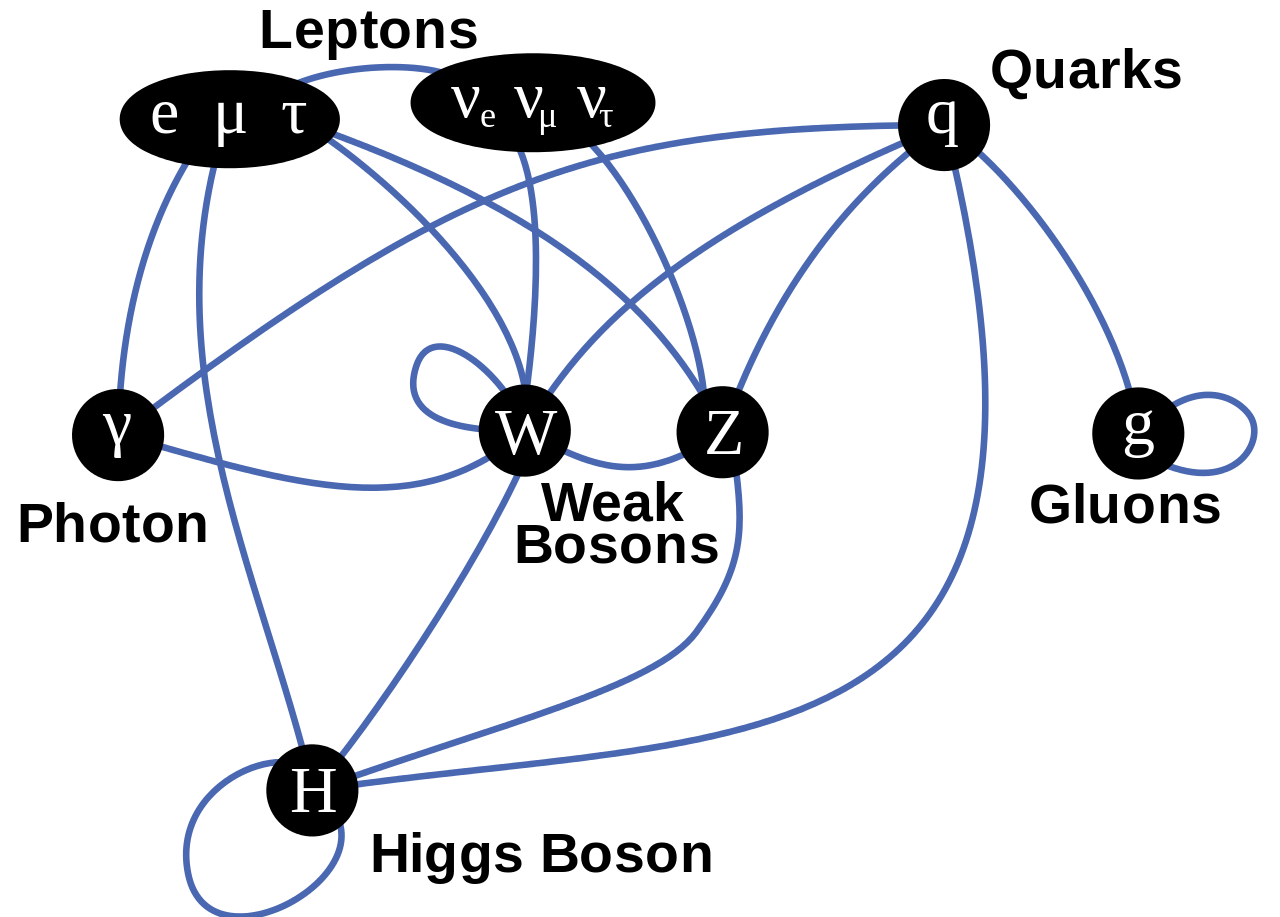
When we look at the Standard Model today, it’s arranged as follows:

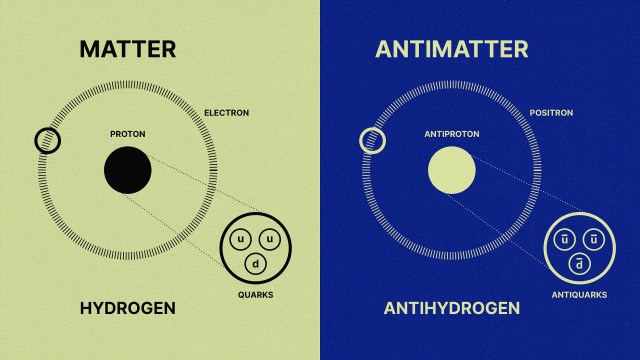
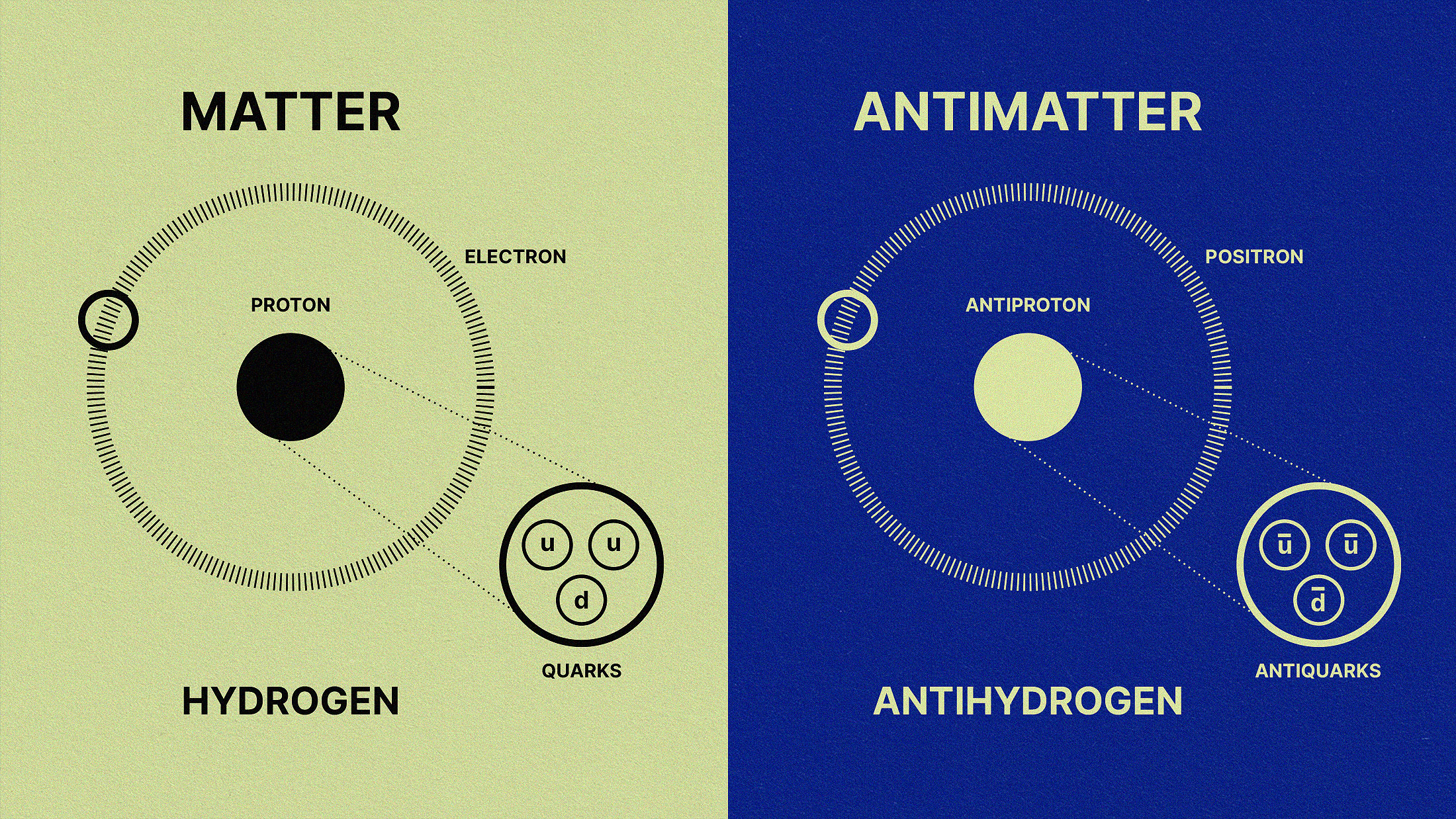
• six quarks, each of which come in three colors, and their antiquark counterparts,
• three charged leptons (e, μ, τ) and three neutral ones (ν_e, ν_μ, ν_τ), and their antimatter counterparts,
• the eight massless gluons that mediate the strong force between the quarks,
• the three heavy, weak bosons (W⁺, W^–, and Z⁰) that mediate the weak nuclear force,
• and the photon (γ), the massless mediator of the electromagnetic force.

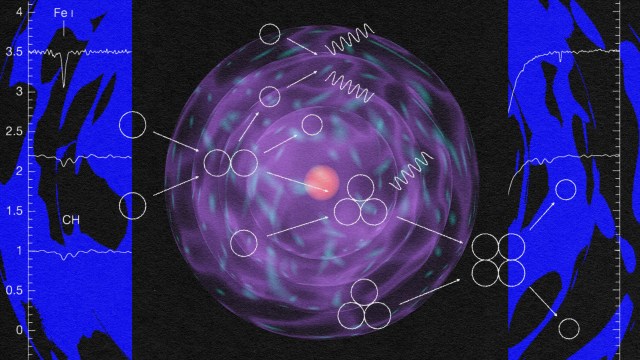
But there’s a symmetry that’s broken at today’s low-energy scale: the electroweak symmetry. This is why there are four fundamental forces, as in addition to gravitation and the strong nuclear force, there are the electromagnetic force and the weak nuclear force, separate and independent from one another. But back in the early days of the Universe, there was a symmetry, the electroweak symmetry, that was fully restored. And when it’s in a restored state versus when it’s in a broken state, it fundamentally changes the Standard Model picture.

The massless W and B bosons, instead of the W+, W-, the Z, and the photon, were the electroweak bosons that existed as the force carriers back before the electroweak symmetry was broken in the early Universe.

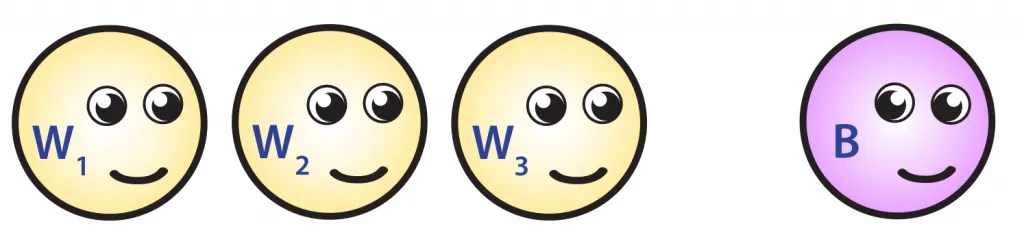
Today, as part of the Standard Model of elementary particle physics, we have the weak and electromagnetic bosons (W⁺, W^–, Z⁰, γ) mediating the weak force and the electromagnetic force. In today’s Universe, the first three are very massive and the last is massless. On the other hand, in the very early stages of the Universe when the electroweak symmetry was restored, we had four new bosons mediating the electroweak force (W₁, W₂, W₃, B), and all of them had no mass at all.

The other Standard Model particles, at this early stage, are all the same as they are today, except for one important fact: they, too, have no mass yet. This is what’s floating around in the early Universe, colliding, annihilating, and spontaneously being created, all in motion at the speed of light.

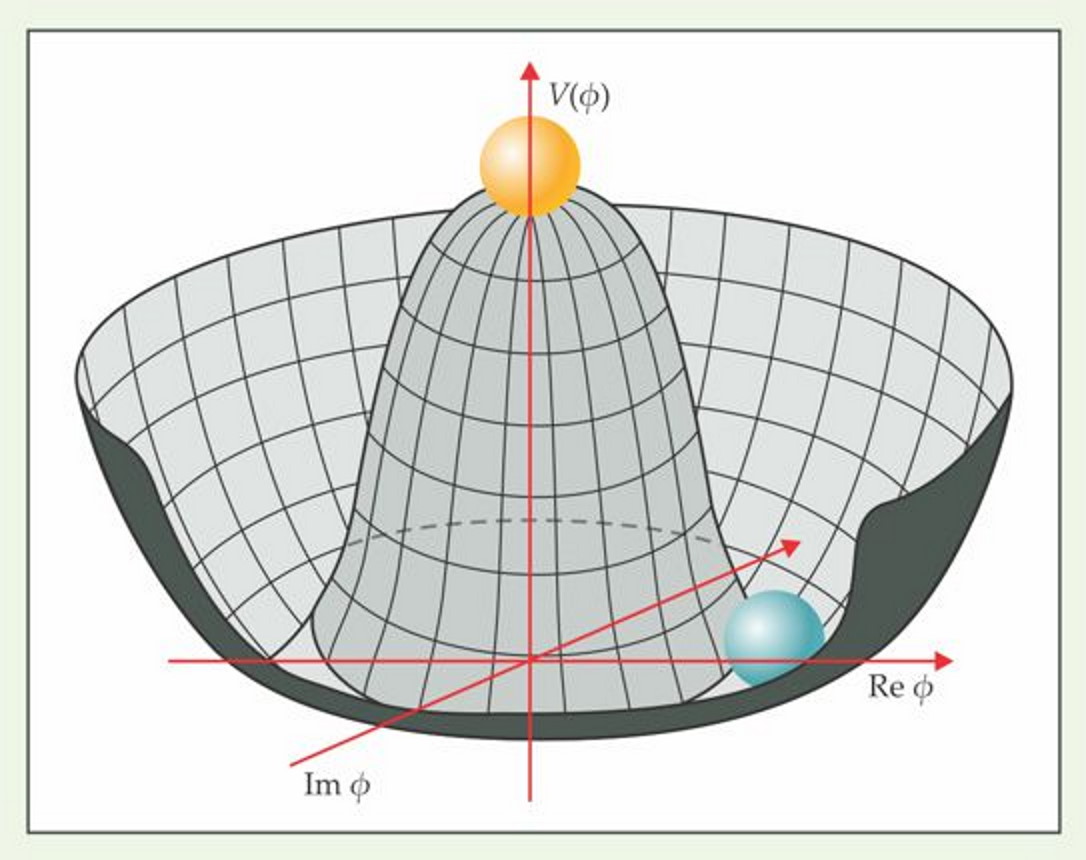
As the Universe expands and cools, all of this continues. So long as the energy of your Universe is above a certain value, you can think about the Higgs field as floating atop the liquid in a soda (or wine) bottle. As the level of the liquid drops, the Higgs field remains atop the liquid, and everything stays massless. This is what we call a restored-symmetry state.

When a wine bottle is either completely or partially filled, a drop of oil or a ping pong ball would float on the wine’s surface inside the bottle. At any location, the wine-level, and hence what’s floating atop it, will remain at the same level. This corresponds to a restored-symmetry state, where all locations and positions lead to equivalent values for whatever field this analogy applies to. Once the level of wine exposes the peak at the bottom of the bottle, the symmetry is no longer restored, and is instead broken.

But below a certain liquid level, the bottom of the container starts to show itself. Once there’s a different level for the liquid to sink to that goes beneath the structure of the bottle itself, the field can no longer remain in the center; more generally, it can’t take on simply any old value. It has to go to where the liquid level is, and that means down into the divot(s) at the bottom of the bottle. This leads to what we call a broken-symmetry state: where different locations have different field values, and where not every possible location has an equal value to each other.

When this symmetry in question, the electroweak (or Higgs) symmetry, breaks, the Higgs field settles into the bottom, lowest-energy, equilibrium state. But that energy state isn’t quite zero: it has a finite, non-zero value known as its vacuum expectation value. Whereas the restored-symmetry state yielded only massless particles, the broken symmetry state changes everything.

When a symmetry is restored (yellow ball at the top), everything is symmetric, and there is no preferred state. When the symmetry is broken at lower energies (blue ball, bottom), the same freedom, of all directions being the same, is no longer present. In the case of the electroweak (or Higgs) symmetry, when it breaks, there’s a spontaneous process that occurs, giving mass to the particles in the Universe.

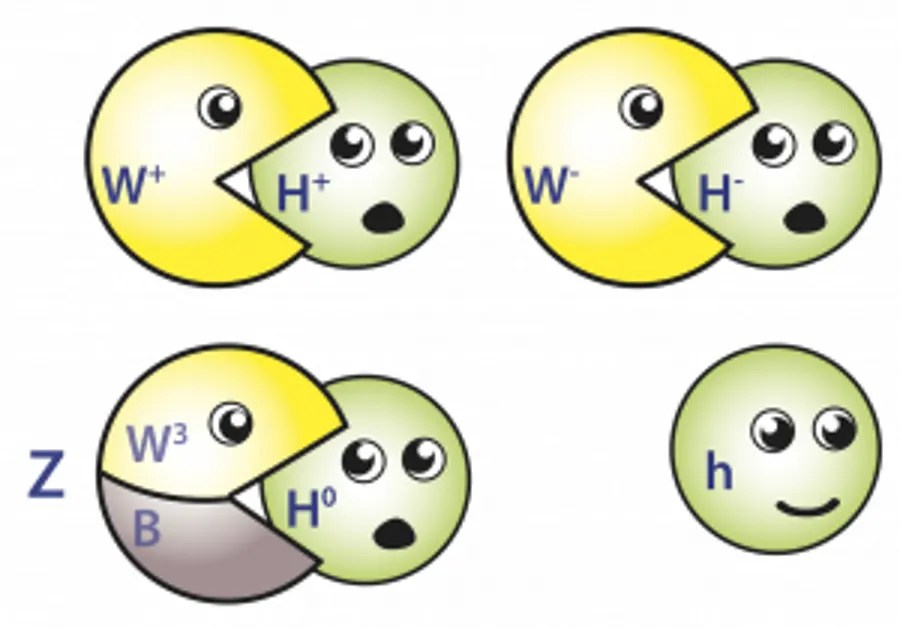
Once the symmetry breaks, the Higgs field has four mass-containing consequences: two are charged (one positive and one negative) and two are neutral. Then, the following things all happen at once:

• The W₁ and W₂ particles “eat” the charged, broken-symmetry consequences of the Higgs, becoming the W⁺ and W^– particles. These are the only bosons that mediate flavor-changes between the Standard Model fermions.
• The W₃ and B particles mix together, with one combination “eating” the uncharged broken-symmetry consequence of the Higgs, becoming the Z⁰, and with the other combination eating nothing, to remain massless and become the photon (γ).
• The last neutral broken-symmetry consequence of the Higgs gains mass, and becomes the Higgs boson.
• At last, the Higgs boson couples to all the other particles of the Standard Model, giving mass to the Universe.

This is where mass comes from, at least, in our Universe.

When the electroweak symmetry is broken, the W+ gets its mass by eating the positively charged Higgs, the W- by eating the negatively charged Higgs, and the Z0 by eating the neutral Higgs. The other neutral Higgs becomes the Higgs boson, detected and discovered earlier this decade at the LHC. The photon, the other combination of the W3 and the B boson, remains massless.

This entire process, involving beginning from a restored-symmetry state and transitioning to a broken-symmetry state, is known as spontaneous symmetry breaking. For the quarks and leptons in the standard model, when this Higgs symmetry is broken, every particle gets a mass due to two things:

1. the expectation value of the Higgs field, and
2. a coupling constant.

And this is kind of the problem. The expectation value of the Higgs field is the same for all of these particles, and not too difficult to determine. But that coupling constant? Not only is it different for every particle, but — in the Standard Model — there’s no way to calculate or predict it. It’s what we call an arbitrary parameter, meaning that, if we want to know its value, we have to go and measure it. There’s no law or rule that dictates what values it ought to have for any of the particles at all.

This diagram of the Standard Model particles shows the fermions in the top row, the gauge bosons in the middle row, and the Higgs on the bottom. The lines indicate couplings, and you can see which fermionic particles couple to which of the forces by the blue lines. Everything with mass couples to the Higgs; the only particles which are massless (and hence, do not) are the photon and the gluons. If there are new particles out there, their couplings may reveal their presence, indirectly, through precision measurements that compare the particles’ observed properties with those predicted by the Standard Model.

We know that the particles have mass; we know how they get mass; we’ve discovered the particles responsible for mass. But we still have no idea why the particles have the values of the masses they do. We have no idea why the coupling constants have the couplings that they do, and unless we find evidence for some idea that takes us beyond the Standard Model into a model that has this predictive power that the Standard Model does not, our only resort is to measure those arbitrary couplings.

The Higgs boson is real; the gauge bosons are real; the quarks and leptons are real. We can create, detect, and measure their properties exquisitely, including their rest masses. Yet, when it comes to understanding why they have the values that they do, that’s a puzzle we cannot yet solve. We do not have the answer.

The rest masses of the fundamental particles in the Universe determine when and under what conditions they can be created, and also relate to how long they can survive after their creation during the hot Big Bang. The more massive a particle is, the less time it can spontaneously be created in the early Universe, and the shorter its lifetime will be.

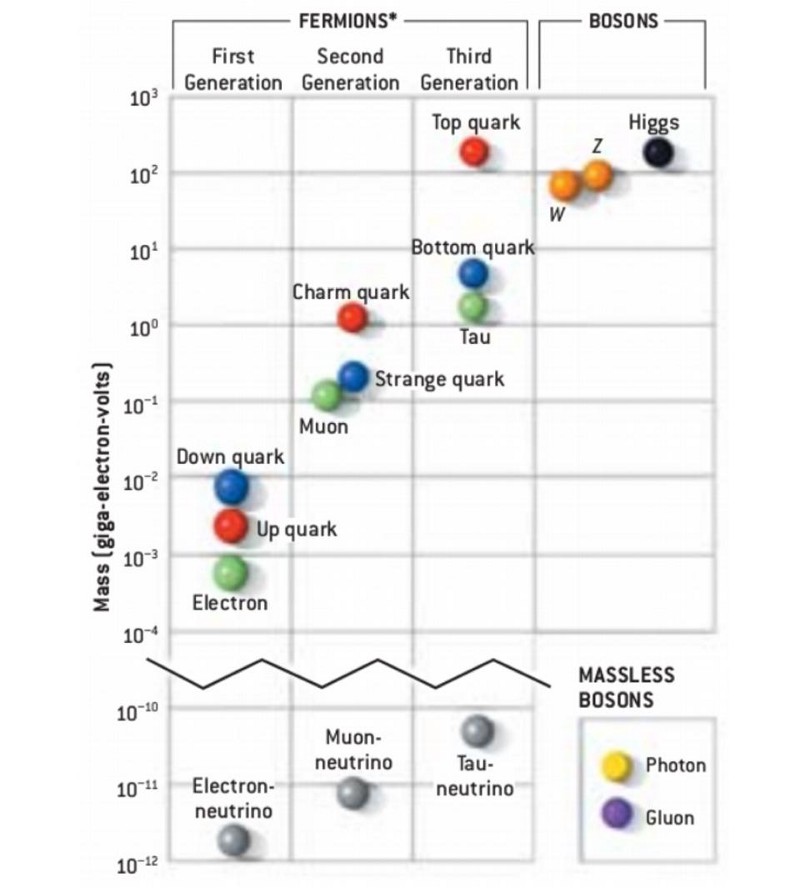
Before the breaking of the electroweak symmetry, everything that is known to exist in the Universe today is massless, and moves at the speed of light. Once the Higgs symmetry breaks, it gives mass to the quarks and leptons of the Universe, the W and Z bosons, and the Higgs boson itself. (At least, we think so. The neutrino sector is complicated, and there may yet be another explanation for why neutrinos have mass that falls outside of the influence of the Higgs.)

Suddenly, with huge mass differences between light particles and heavy ones, the heavy ones spontaneously decay into the lighter ones on very short timescales, especially when the energy (E) of the Universe drops below the mass equivalent (m) needed to create these unstable particles via E = mc².

A visual history of the expanding Universe includes the hot, dense state known as the Big Bang and the growth and formation of structure subsequently. The full suite of data, including the observations of the light elements and the cosmic microwave background, leaves only the Big Bang as a valid explanation for all we see. As the Universe expands, it also cools, enabling ions, neutral atoms, and eventually molecules, gas clouds, stars, and finally galaxies to form. Without the Higgs giving mass to the particles in the Universe at a very early, hot stage, none of this would have been possible.

Without this critical gauge symmetry associated with electroweak symmetry breaking, existence wouldn’t be possible, as there do not exist any known stable, bound states made up purely of massless particles. But in the aftermath of electroweak symmetry breaking and the Higgs coupling to the quarks and leptons in the Universe, they’re now compelled to have fundamental masses: positive, non-zero, and measurable. With rest masses now belonging to the quarks and charged leptons, the Universe can now do a series of things that it’s never done before.

• It can cool and create bound states like protons and neutrons.
• It can cool further and create atomic nuclei and, eventually, neutral atoms.
• And when enough time goes by, these massive, neutral entities can form gravitationally bound states as well.

These composite, bound, neutral states can then give rise to stars, galaxies, planets, and human beings. Without the Higgs to give mass to the Universe, none of this would be possible. The Higgs, despite the fact that it took 50 years to discover from when it was proposed to when it was robustly detected, has never taken even a moment off. It’s been making the Universe possible for 13.8 billion years.