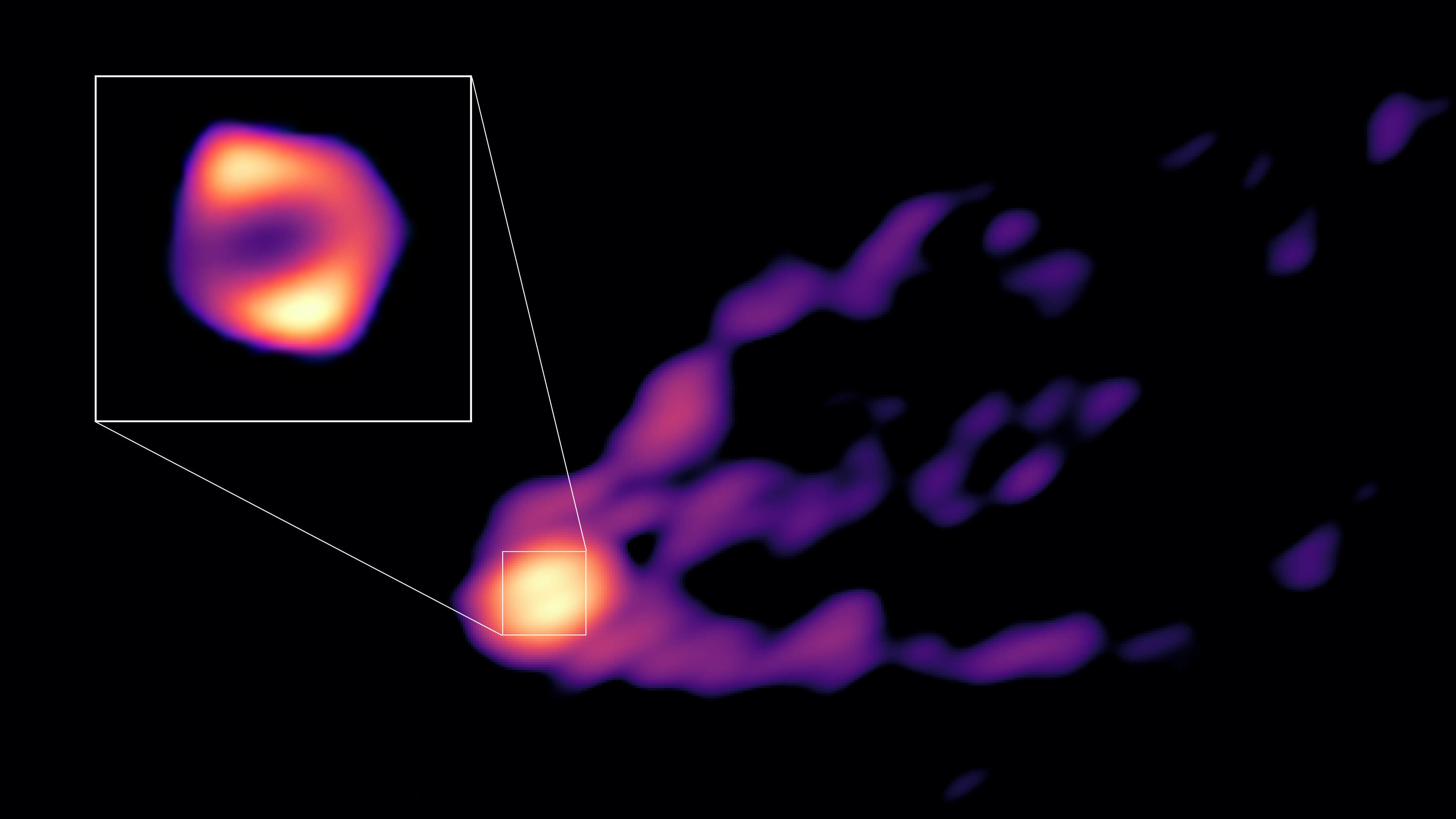
Oppenheimer’s forgotten astrophysics research explains why black holes exist

The 1930s were a fascinating and contentious time: both on the global stage and for the science of nuclear physics. Economically, the great depression led to increases in unemployment, dramatic dropoffs in global industrial production, foreign trade, per-capita GDP, and a rising tide of fascism. But amidst those geopolitical events, a very small revolution was occurring in fundamental physics: a voyage into the atomic nucleus. All around the world, physicists were putting together the puzzle pieces of nuclear physics, including radioactivity, the discovery of the neutron, the energy potential within all matter of E = mc², and the physical processes of fusion and fission.

Before J. Robert Oppenheimer became the leader of the Manhattan Project — i.e., the development of the atomic bomb — he was one of many scientists studying the implications of nuclear physics under some of the most extreme conditions imaginable: during the gravitational collapse of the most massive stars in the Universe. In a series of papers in the late 1930s, Oppenheimer became part of the first team ever to determine the limit to how massive a single atomic nucleus, what we know today as the core of a neutron star, could be before collapsing entirely into what he then called a “dark star,” or in today’s terms, a black hole.

Although he’s much better known for spearheading the United State’s nuclear weapons development program, his astrophysics legacy lives on today as a key component in our understanding of black holes and their formation. Here’s the story you won’t hear in Christopher Nolan’s wildly successful biopic, Oppenheimer.

This cutaway showcases the various regions of the surface and interior of the Sun, including the core, which is the only location where nuclear fusion occurs. As time goes on and hydrogen is consumed, the helium-containing region in the core expands and the maximum temperature increases, causing the Sun’s energy output to increase. When both hydrogen and helium are exhausted within the fusion-rich core region, the star will die.

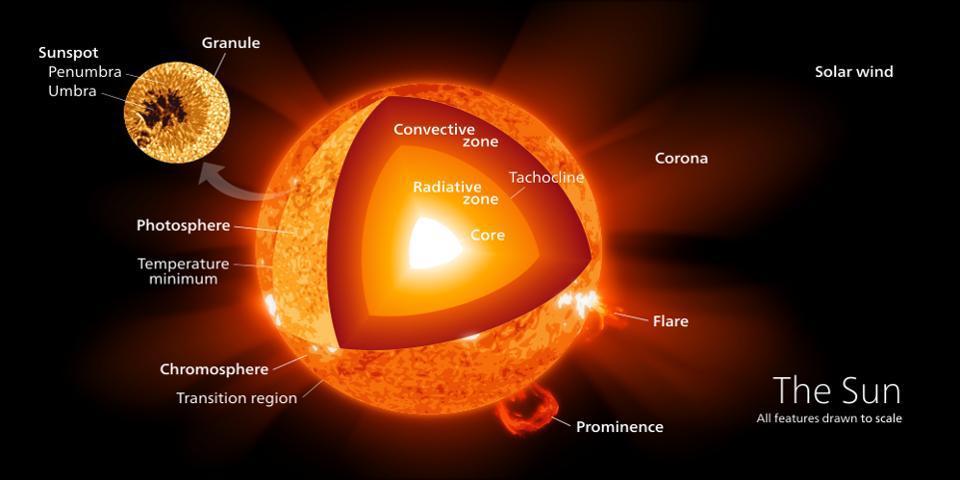
Imagine a star: an enormous collection of mass, dominated by hydrogen with a substantial fraction of helium (plus a small amount of all other elements), with the tremendous force of gravity working to pull that mass inexorably inward. An important question that had been bothering physicists for a very long time was a very simple one: why don’t these objects gravitationally collapse?

A star like our Sun, for example, has some ~300,000 times the mass of the Earth, and yet is somehow only about one-quarter as dense as our planet. In order for that to be the case, there must be some sort of internal force, generated within the Sun itself, pushing back — successfully — against gravitation.

What could that force be? It couldn’t be chemical combustion, as the Sun would have a lifetime measured in the thousands of years, rather than billions, as required by the abundant geological evidence. It couldn’t be from gravitational contraction, as the low density of the Sun would forbid it. And it couldn’t be from some sort of ongoing fuel replenishment, as the added mass would noticeably alter the orbits of the inner planets. There must be some sort of new reaction occurring in the star’s core: a reaction involving nuclear forces.

The most straightforward and lowest-energy version of the proton-proton chain, which produces helium-4 from initial hydrogen fuel. Note that only the fusion of deuterium and a proton produces helium from hydrogen; all other reactions either produce hydrogen or make helium from other isotopes of helium.

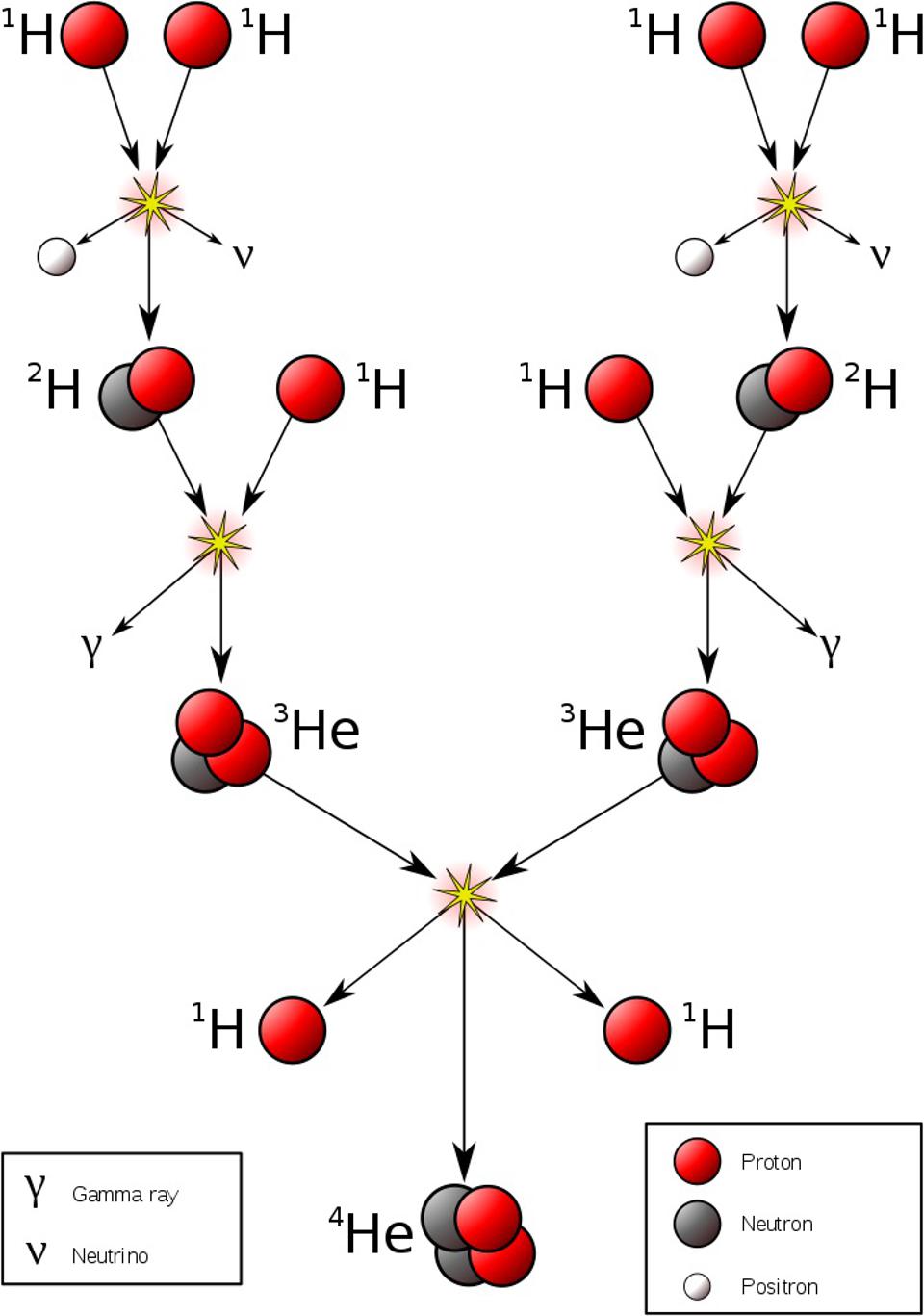
A strong hint of this came simply by looking at two facts together:

1. the composition of the Sun and stars, made mostly of hydrogen and secondarily of helium,
2. and the relative masses of hydrogen and helium nuclei, where one helium-4 nucleus is actually about 0.7% lower in mass than four hydrogen-1 nuclei.

Under the extreme pressures and temperatures created in the core of a star, it would be possible for a series of nuclear reactions to occur, leading to a chain reaction where hydrogen nuclei get eventually converted into helium nuclei, releasing energy — via Einstein’s E = mc² — in the process.

That released energy, as many scientists would work out, could be capable of providing a tremendous amount of outward radiation pressure, causing the Sun (and most stars) to shine for very long time periods, including for billions of years or even longer, while simultaneously holding the star (including the Sun) up against gravitational collapse. While most scientists working on this problem set about to understand the nuclear reactions occurring in gory detail, Oppenheimer was more interested in a different aspect of the problem: what would happen to a star when it fully exhausted the nuclear fuel it was burning to hold itself up against gravitational collapse?

The Sun, when it becomes a red giant, will become similar in size to Arcturus. Antares is more of a supergiant star and is much larger than our Sun (or any Sun-like stars) will ever become. Even though red giants put out far more energy than our Sun, they are cooler and radiate at a lower temperature at their surfaces. Inside their cores, where helium fusion occurs, temperatures can rise into the tens of millions of K.

Oppenheimer knew part of the story: that without a source of fuel left to continue generating radiation, gravitation would gain the upper hand, and the core of the star would begin to contract. Any physical system that compresses or contracts rapidly — without enough time for heat to be exchanged between the interior and exterior environments — will increase in temperature, as the same amount of total heat gets compressed into a smaller and smaller volume.

With our modern knowledge of nuclear physics, we now know that increasing the temperature of the helium-rich core of a massive star will cause it to initiate helium fusion: the process of fusing three helium-4 atoms into an excited state of carbon-12, which releases even more energy than fusing hydrogen-into-helium released previously. Stars that are more-or-less as massive as our Sun will eventually initiate helium fusion, but that just pushes the inevitable problem further down the road: what then happens when a star runs out of helium fuel in its core?

Eventually, again, it runs out of radiation, and the core begins to gravitationally contract, heating it up even further.

By siphoning mass off of a companion star, a stellar corpse like a white dwarf can eventually accrue enough material to exhibit a thermonuclear runaway event, resulting in a nova. Only if the white dwarf itself exceeds a critical mass threshold, the Chandrasekhar limit, will a type Ia supernova ensue, and this type of “siphoning” may not be the main pathway for such supernovae to occur, but rather the mergers of two white dwarfs might be the primary trigger.

Some stars, like our Sun, won’t heat up to be hot enough to initiate any further nuclear burning reactions, and so the core, made largely of elements like carbon and oxygen (which can be created if a carbon atom fuses with a helium atom), simply contracts and contracts until it can contract no further. There’s a limit to how far the star can contract, set not by the thermal radiation pressure of a living star, but rather by a quantum mechanical effect: the electron degeneracy pressure of the ionized electrons floating about the sea of atomic nuclei.

Because no two electrons — an example of a type of particle known as a fermion — can occupy the same quantum state, as forbidden by the Pauli exclusion principle, these types of stellar remnants can hold themselves up against gravitational collapse. These stellar remnants would be physical objects, with higher temperatures and densities at their cores than at the outskirts, and correspond to what’s known in modern times as a white dwarf.

However, there must be a limit to how massive a white dwarf can be, as beyond a certain mass, the size of the white dwarf would be predicted to collapse to zero: a wholly unphysical value. Once a critical density is achieved, either further nuclear reactions must take place or the white dwarf must collapse further, leading to a black hole. That mass limit was first worked out by Subrahmanyan Chandrasekhar in 1930 and has been known as the Chandrasekhar mass limit ever since.

In the inner regions of a star that undergoes a core-collapse supernova, a neutron star begins to form in the core, while the outer layers crash against it and undergo their own runaway fusion reactions. Neutrons, neutrinos, radiation, and extraordinary amounts of energy are produced, with neutrinos and antineutrinos carrying the majority of the core-collapse supernova’s energy away.

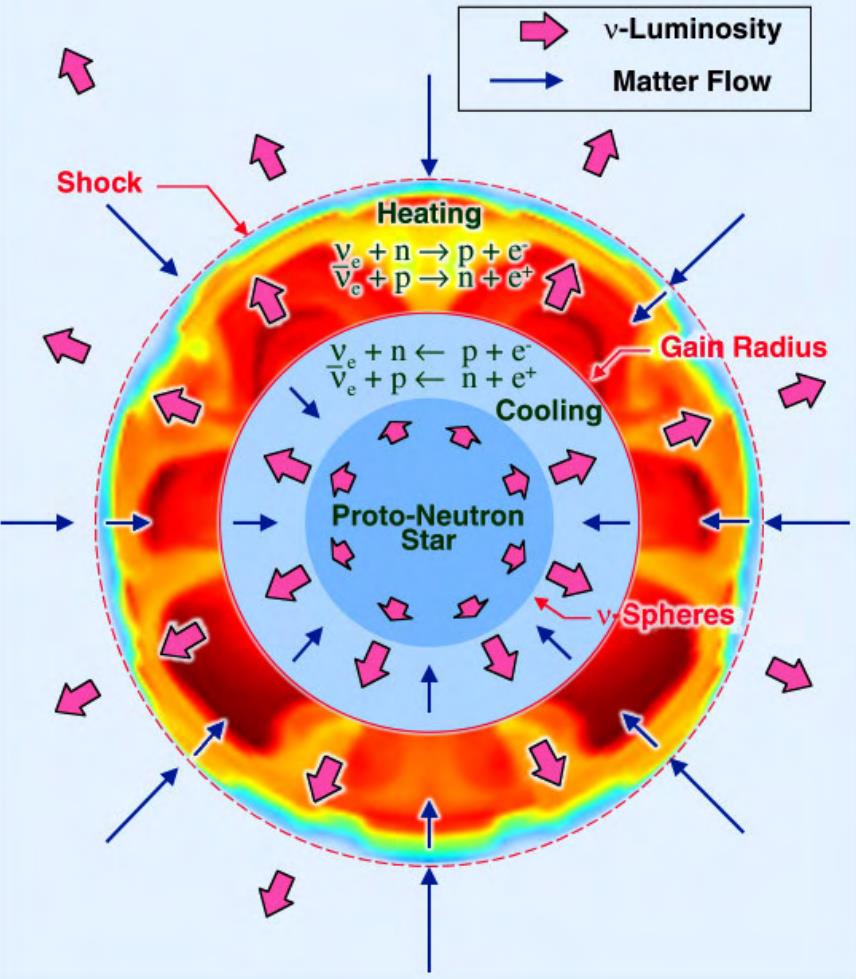
But Oppenheimer chose to consider a different aspect of this problem: what would happen to the most massive stars, the ones where temperatures and densities rose to arbitrary heights after burning through both their hydrogen and helium fuel sources?

The detailed answer wouldn’t be worked out for several decades. When a massive enough carbon core of a star contracts, it gets hot enough to initiate carbon fusion, which creates elements like neon. As the neon core then contracts and heats up, neon-burning occurs at even higher temperatures, photodisintegrating (being blasted apart by a high-energy photon) into oxygen. Again, the core contracts and rises in temperature, leading to oxygen fusion, producing elements like silicon and sulfur. When the core then contracts further, having exhausted its oxygen, silicon-burning occurs, building up elements through helium capture into sulfur, argon, calcium, titanium, chromium, iron, and nickel. At this point, the core becomes inert, and a core-collapse supernova will soon follow.

A white dwarf, a neutron star, or even a strange quark star are all still made of fermions. The Pauli degeneracy pressure helps hold up the stellar remnant against gravitational collapse, preventing a black hole from forming. Inside the most massive neutron stars, an exotic form of matter, a quark-gluon plasma, is thought to exist, with temperatures rising up to ~1 trillion (10^12) K inside.

Although Oppenheimer didn’t know these details, he did come to an important realization. Whatever nuclear reactions did occur would eventually run into a limit: the limit of having the entire core of the star behave as one single atomic nucleus, and that nucleus would inevitably possess a limit as to how massive it could be. Compress a proton and an electron under high enough temperatures and pressures, and it will become a neutron through the process of electron capture, radiating a ghostly neutrino away in the aftermath.

Progress on this front came exceptionally rapidly: James Chadwick experimentally discovered the neutron in 1932, and the very next year, both Walter Baade and Fritz Zwicky (yes, the Fritz Zwicky of dark matter fame) suggested that neutron stars would be created in the aftermath of a massive star’s collapsing death throes.

This was the problem that Oppenheimer was obsessed with in the 1930s: take a neutron star, as massive as you like, and compress it further by whatever means you like. Add mass to it, decrease its volume, simply put more neutron star matter together in one place, etc. At some point, you’re going to hit the same type of limit that Chandrasekhar hit for white dwarfs, but for neutron stars.

In the final moments of merging, two neutron stars don’t merely emit gravitational waves, but a catastrophic explosion that echoes across the electromagnetic spectrum. Whether it forms a stable neutron star or a black hole (like the 2019 merger), or a neutron star that then turns into a black hole (like the 2017 merger), will depend on factors like the total mass of the predecessor neutron stars and their combined spin.

Oppenheimer, building upon previous work by Richard Tolman and working in collaboration with George Volkoff, reasoned that the same physical effect must come into play. Whether it’s a group of neutrons, protons, or electrons doesn’t matter, as they’re all examples of fermions, and they all obey the Pauli exclusion principle: no two of them, in the same place at the same time, can occupy the same quantum state. This creates a degeneracy pressure that pushes outward, preventing the stellar remnant — whether neutron star or white dwarf — from surpassing a certain critical value for their mass.

The equation governing that maximum mass value for the simplest model of a neutron star, one that was cold and non-rotating, was first worked out by Oppenheimer and Volkoff, and is today known as the Tolman-Oppenheimer-Volkoff limit, or just the TOV limit for short. When modern nuclear and particle physics is taken into account, including the fact that neutrons are composite particles made up of the more fundamental quarks and gluons and are governed by the strong nuclear force, the same equations and approach that Oppenheimer and Volkoff used way back in 1939 are still used today, that there’s a maximum possible mass for a non-rotating neutron star of somewhere around 2.2-to-2.9 solar masses.

The most up-to-date plot, as of November 2021 (past the end of LIGO’s third data run but before the start of the fourth), of all the black holes and neutron stars observed both electromagnetically and through gravitational waves. While these include objects ranging from a little over 1 solar mass, for the lightest neutron stars, up to objects a little over 100 solar masses, for post-merger black holes, gravitational wave astronomy is presently only sensitive to a very narrow set of objects. The closest black holes had all been found as X-ray binaries, until the November 2022 discovery of Gaia BH1. The mass “border” between neutron stars and black holes is still being determined.

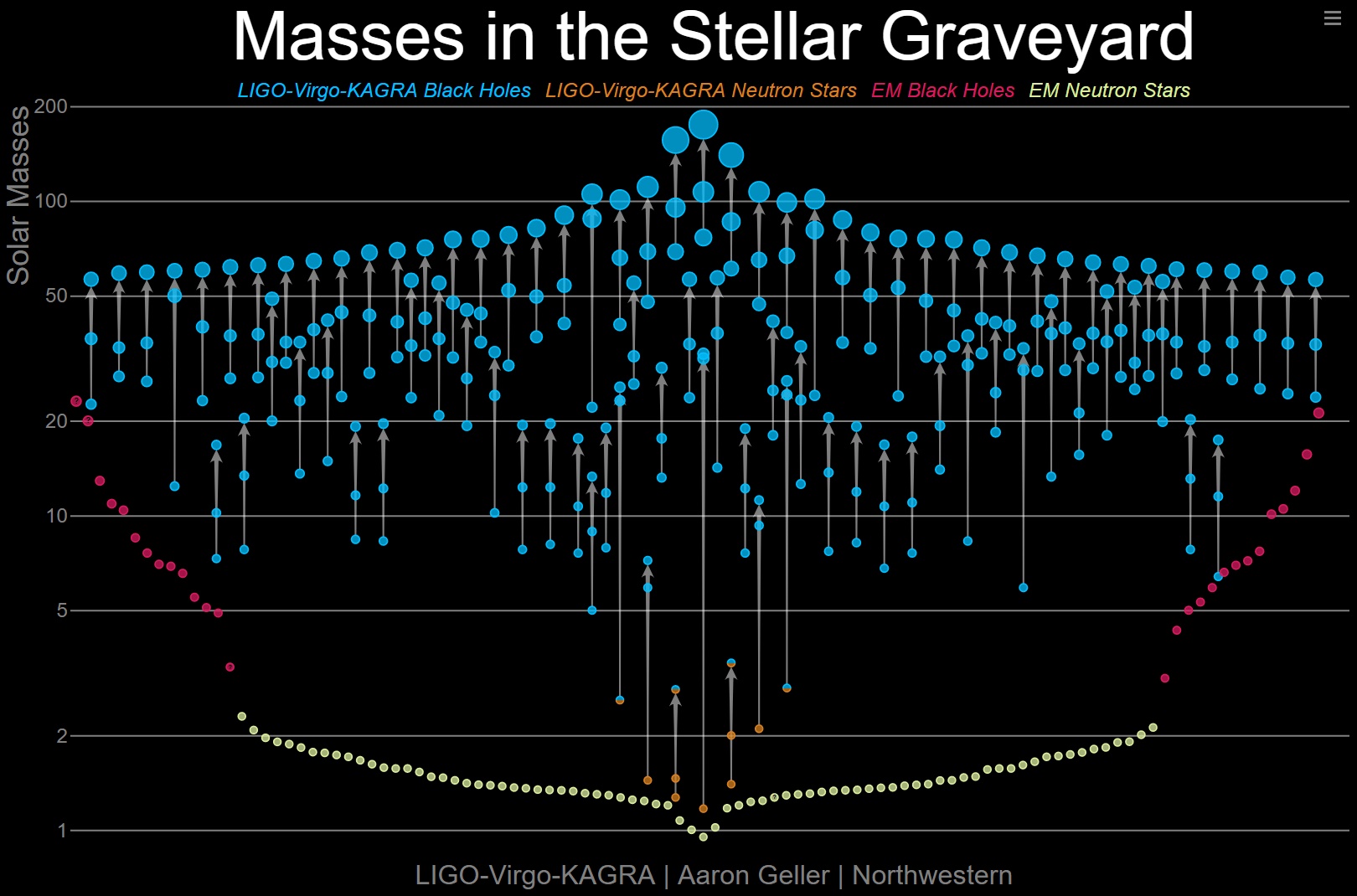
How do the modern-day predictions that grew out of Oppenheimer’s work stack up to the best modern-day observations we have for neutron stars? Outstandingly well. I would encourage anyone interested in neutron star limits not to consult Wikipedia’s list of the most massive neutron stars, as that list is dominated by neutron stars with substantial mass (and distance) uncertainties, but rather to note the following three extremely precise observations.

1. The most massive neutron star with an accurate distance and mass measurement is the millisecond pulsar PSR J0740+6620, which although it’s rapidly rotating, has a very well-measured mass of 2.08 solar masses, with an uncertainty of only about 3% on that value: just a little bit below the TOV limit.
2. In 2017, the LIGO-Virgo collaborations observed the first neutron star-neutron star merger ever seen: GW170817, where the combined mass of the predecessor neutron stars was about 2.75 solar masses. They briefly formed a (possibly rapidly rotating) neutron star for less than a second, before collapsing to a black hole.
3. And in 2019, the LIGO-Virgo collaborations observed the second neutron star-neutron star merger ever seen, but with a higher combined mass of between 3.3-3.7 solar masses: GW190425. This time, the post-merger remnant went straight to a black hole, indicating no neutron star intermediary.

This computer simulation of a neutron star shows charged particles being whipped around by a neutron star’s extraordinarily strong electric and magnetic fields. It is possible that a neutron star has formed within the remnant of SN 1987A, but the region is still too dusty and gas-rich for the “pulses” to seep out.

It’s a very difficult task to find the highest mass neutron star and the lowest mass black hole, as pinning down the properties of these objects is notoriously difficult due to their relative rarity (compared to stars), their distance (typically thousands of light-years from us or more), their low or even null brightnesses, and the fact that the extreme objects — the highest-mass neutron stars and the lowest-mass black holes — are exceedingly rare. Nevertheless, with ever-improving pulsar timing technology, the discovery of new neutron stars within the Milky Way, and more examples of neutron star-neutron star mergers forthcoming, we may find ourselves closing in on discovering where the neutron star/black hole mass limit lies, as well as its spin-dependence.

However, whenever we remember Oppenheimer, it shouldn’t be exclusively for his personal life, his political stances, or even his role in the development of the atomic bomb. Instead, it’s arguable that his most lasting contribution to the world, from a scientific perspective, is an astrophysical one: developing the method for theoretically understanding the upper mass limit that defines the border between a neutron star and a black hole.

For when Oppenheimer quotes the Bhagavad Gita and states, “Now I am become Death, the destroyer of worlds,” he may as well have referred to every neutron star that was or would’ve been, but was too massive to do anything other than collapse down: all the way to a singularity.