The periodic table you grew up with is wrong
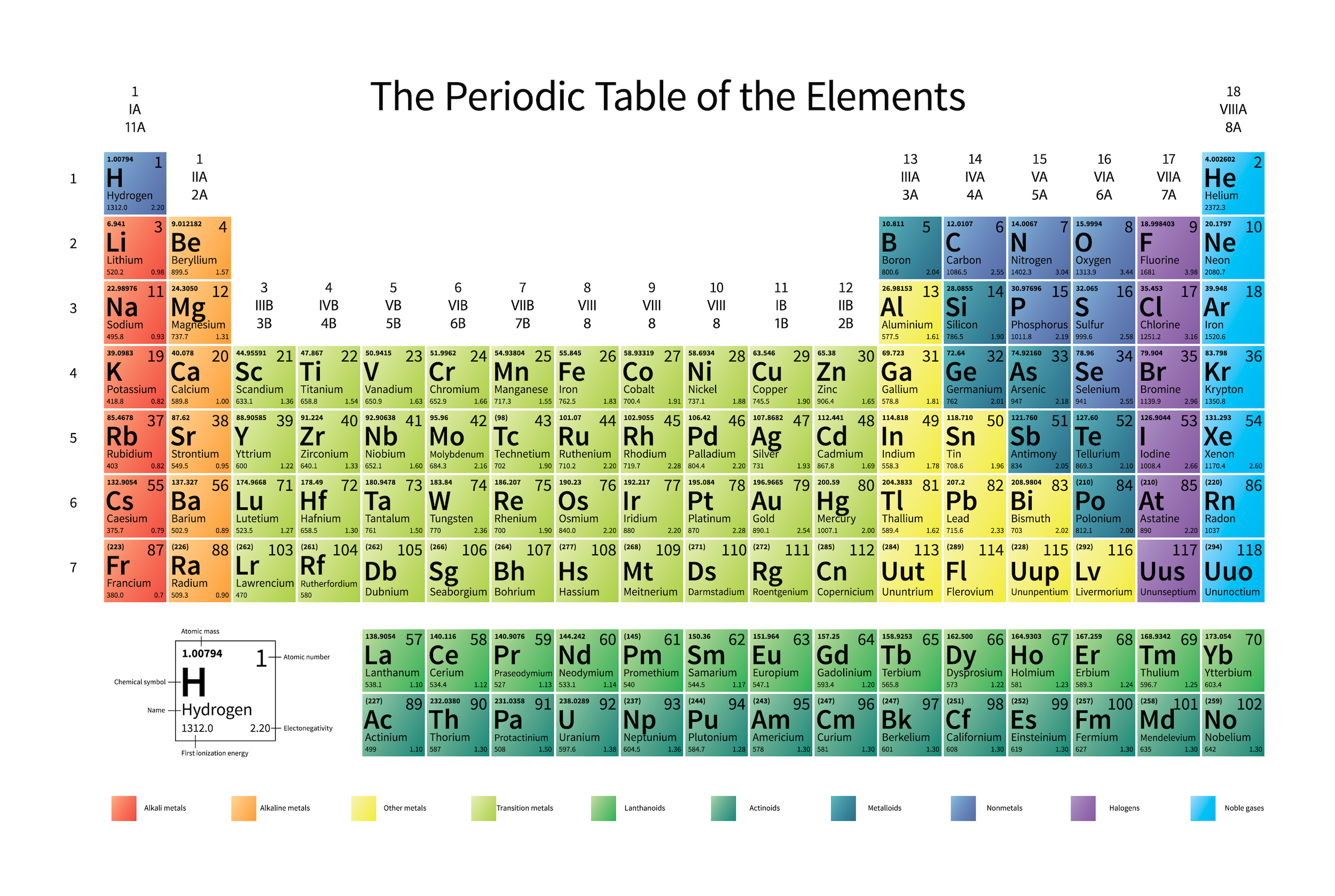
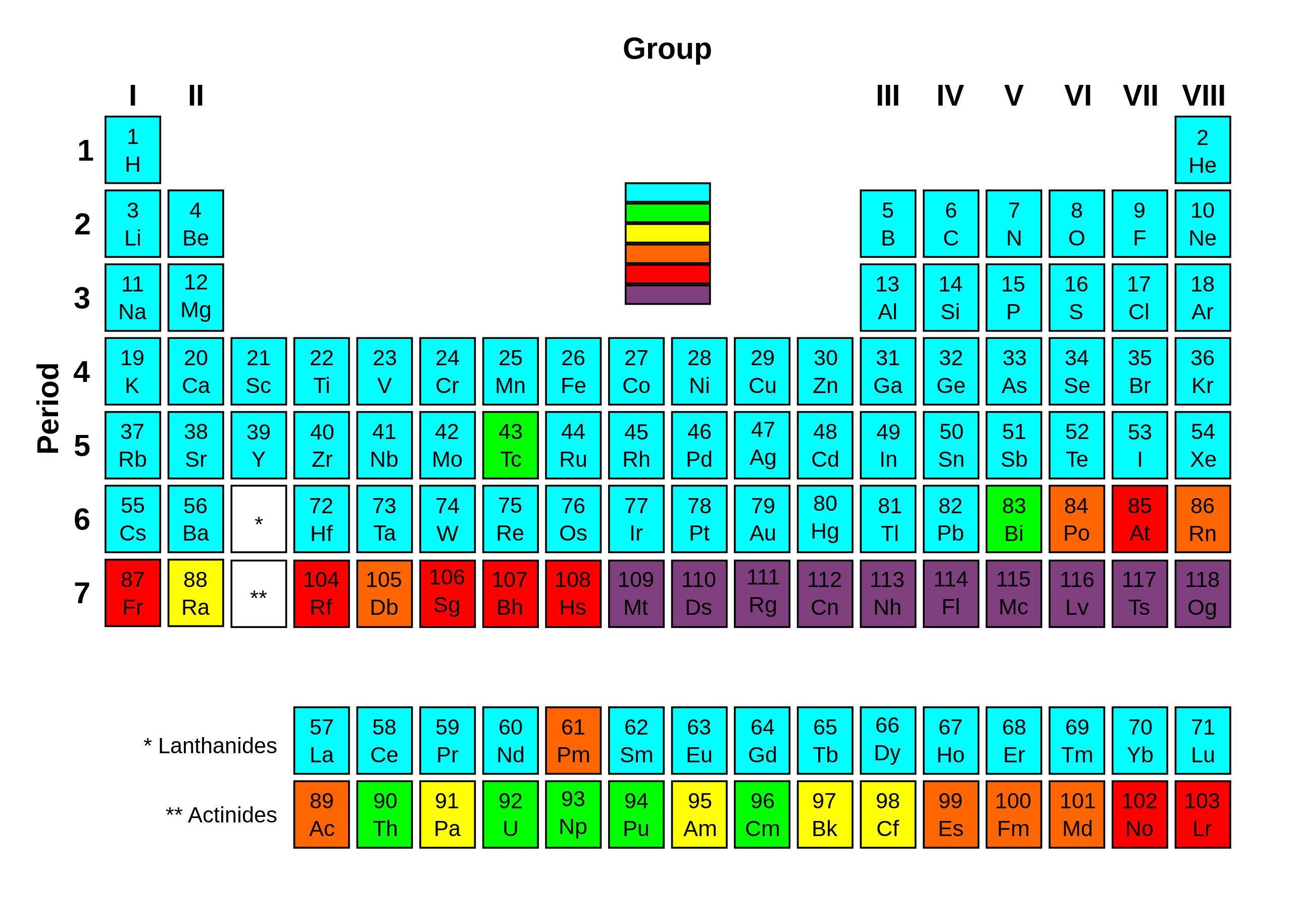
- The elements of the periodic table are sorted by their elemental properties, defined by the number of protons in the nucleus and the bonds formed by their electron structures.
- Up until the early 2000s, we thought that the heaviest stable element was bismuth: the 83rd entry on the periodic table.
- However, we recently learned that bismuth is inherently unstable, and decays after ~10^19 years. Are lead and the other heavy elements truly stable, or if we wait long enough, will everything eventually decay?
As we came to observe the Universe on smaller and more fundamental scales, we began to discover what the building blocks of matter were. Macroscopic materials are made up of smaller components that still retain the physical and chemical properties of the larger original. You can break things down into individual molecules, and still those molecules will exhibit the same behavior in isolation as they did when they were part of the larger structure. Molecules can be broken down further, into individual atoms, which still retain the same binding properties they possessed when they were in molecules: evidence that there’s something very important, on the atomic level, for building up the larger-scale structures in our Universe today.
We eventually came to recognize that atoms have properties that can be sorted, periodically, by the number of protons in their nucleus. The positive charges in the nucleus determine how many electrons must orbit that nucleus to make an electrically neutral atom, and then the behavior of those electrons, according to the laws of quantum physics, determine how those atoms behave, interact, and bind together. The periodic table of elements is taught across schools worldwide. There’s just one problem: if you learned the elements from a periodic table made before 2003, there’s a glaring error within it. Here’s what everybody should know.

Within the core of every atom lies an atomic nucleus: a tightly bound, massive structure composed of at least one proton and, in all cases except one, multiple neutrons as well. While most of the atoms that make up the everyday world we experience are known to be stable, there are many combinations of protons-and-neutrons that are inherently unstable, and will decay away into a different element if enough time is allowed to pass.
For some elements, like carbon, there are multiple stable isotopes, as carbon-12 (with 6 protons and 6 neutrons) is stable, as is carbon-13 (with 6 protons and 7 neutrons). However, you can also have carbon-14, with 6 protons and 8 neutrons, which is not stable, but given enough time, will radioactively decay by emitting an electron, an anti-electron neutrino, and transforming one of its neutrons into a proton: becoming nitrogen-14 in the process. Nitrogen-14, with 7 protons and 7 neutrons in its nucleus, is absolutely stable, as is another isotope of nitrogen: nitrogen-15, with 7 protons and 8 neutrons.
Although there are many elements that have one or more stable isotopes, there are a few elements that have none: technetium and promethium are two examples of elements that are always unstable.
It’s actually a relatively novel idea that any form of matter would be unstable: something that only arose as a necessary explanation for radioactivity, discovered in the late 1800s. Materials that contained certain elements — radium, radon, uranium, etc. — appeared to spontaneously generate their own energy, as though they were powered by some sort of internal engine inherent to their very nature.
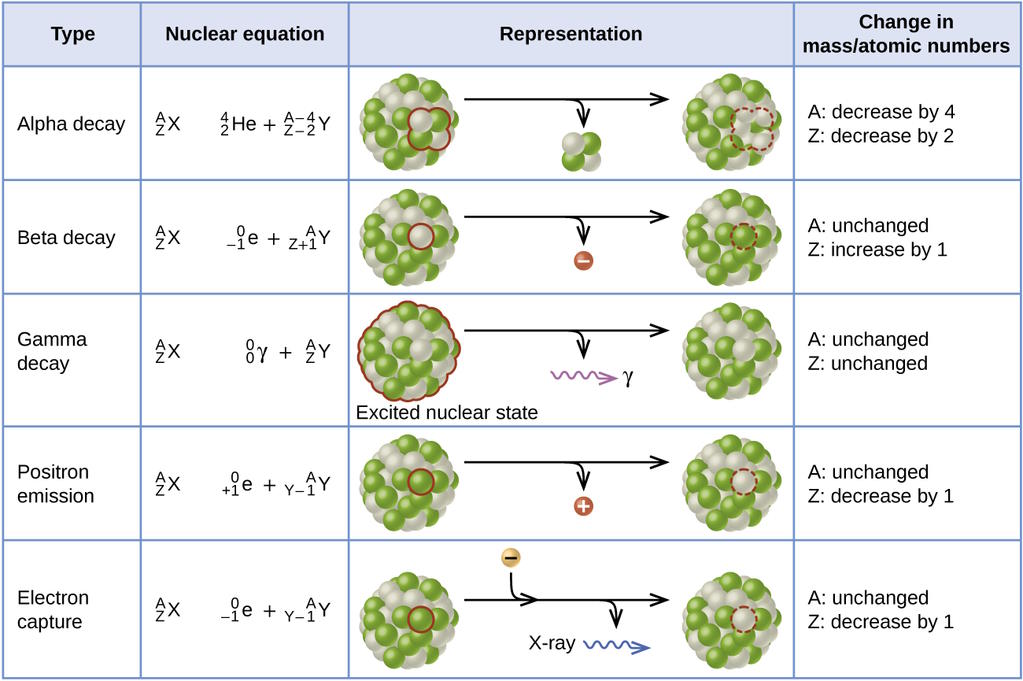
Over time, the truth about these reactions was uncovered: the nuclei of these atoms were undergoing a series of radioactive decays. The three most common types were:
- α (alpha) decay: where an atomic nucleus spits out an α-particle (with 2 protons and 2 neutrons), moving down 2 elements on the periodic table,
- β (beta) decay: where an atomic nucleus converts a neutron into a proton while spitting out an electron (a β-particle) and an anti-electron neutrino, moving up 1 element on the periodic table,
- γ (gamma) decay: where an atomic nucleus, in an excited state, spits out a photon (a γ-particle), transitioning to a lower-energy state.
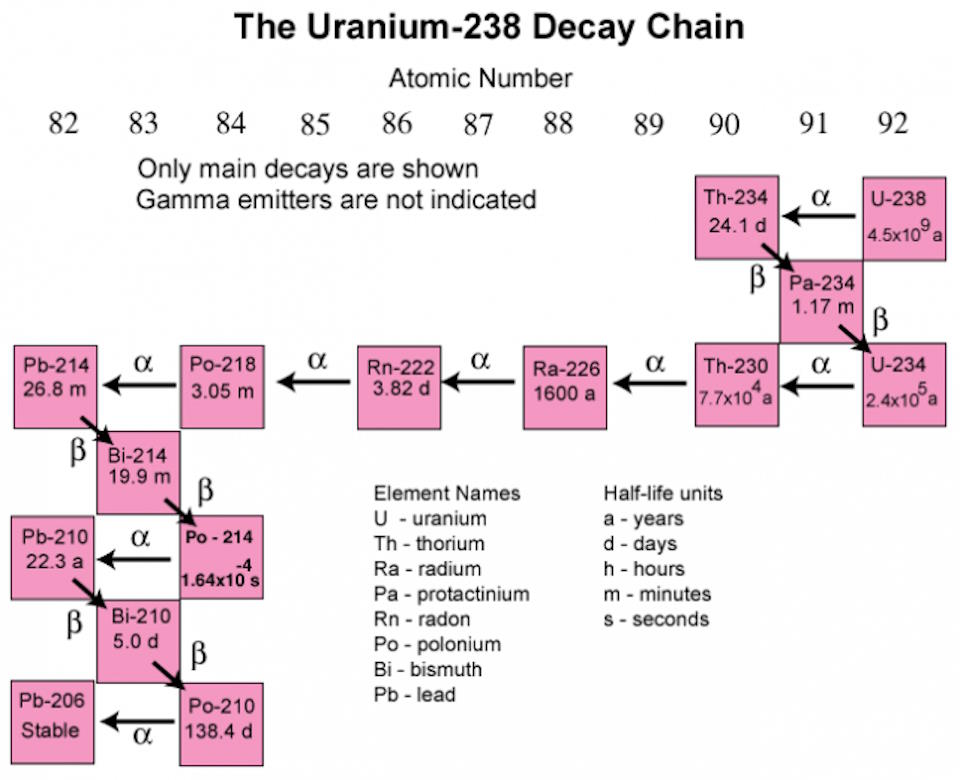
The example of carbon-14 decaying to nitrogen-14 is an example of beta decay, while uranium-238 decaying to thorium-234 is an example of alpha decay.
At the end of these reactions, the total mass of what’s left over (the products) is always less than the total mass of what we began with (the reactants), with the remaining mass converted into pure energy via Einstein’s famous equation, E = mc².
If you learned about the periodic table prior to 2003, you probably learned that bismuth, the 83rd element, was the heaviest stable element, with every element heavier than that undergoing some form of radioactive decay (or decay chain) until a truly stable element is reached.
But in 2003, scientists discovered that every single isotope of bismuth is inherently unstable, including the abundant, naturally occurring bismuth-209. It’s extremely long-lived, with a half-life of around ~1019 years: approximately one billion times the age of the present Universe. Since that discovery, the structure of the periodic table was changed to reflect that bismuth, although incredibly long-lived, is now known not to be stable at all. Instead, those tables now (correctly, to the best of our knowledge) report that lead, the 82nd element, is the heaviest stable element known.
The reason that radioactive decays occur wasn’t well understood for many decades after the discovery of radioactivity: it’s an inherently quantum process. There are certain conservation rules that are an inextricable part of the laws of physics, as quantities like energy, electric charge, and linear and angular momentum are always conserved. That means, if we were to measure those properties for both the reactants and the products (or the physically possible products) of any candidate reaction, they must always be equal. These quantities cannot be spontaneously created or destroyed; that’s what it means to be “conserved” in physics.
But if there are multiple configurations that are allowed that obey all of those conservation rules, there’s a way to determine which configuration(s) are more stable relative to the others: some of them will be more energetically favorable. “Energetically favorable” is like being a round ball on top of a hill and rolling down it. Where will it come to rest? At the bottom, right? Not necessarily. There can be many different low-points where the ball can wind up — what we know as “false minima” in science — where only one of them will be the absolute lowest-energy configuration of all: the true minimum.
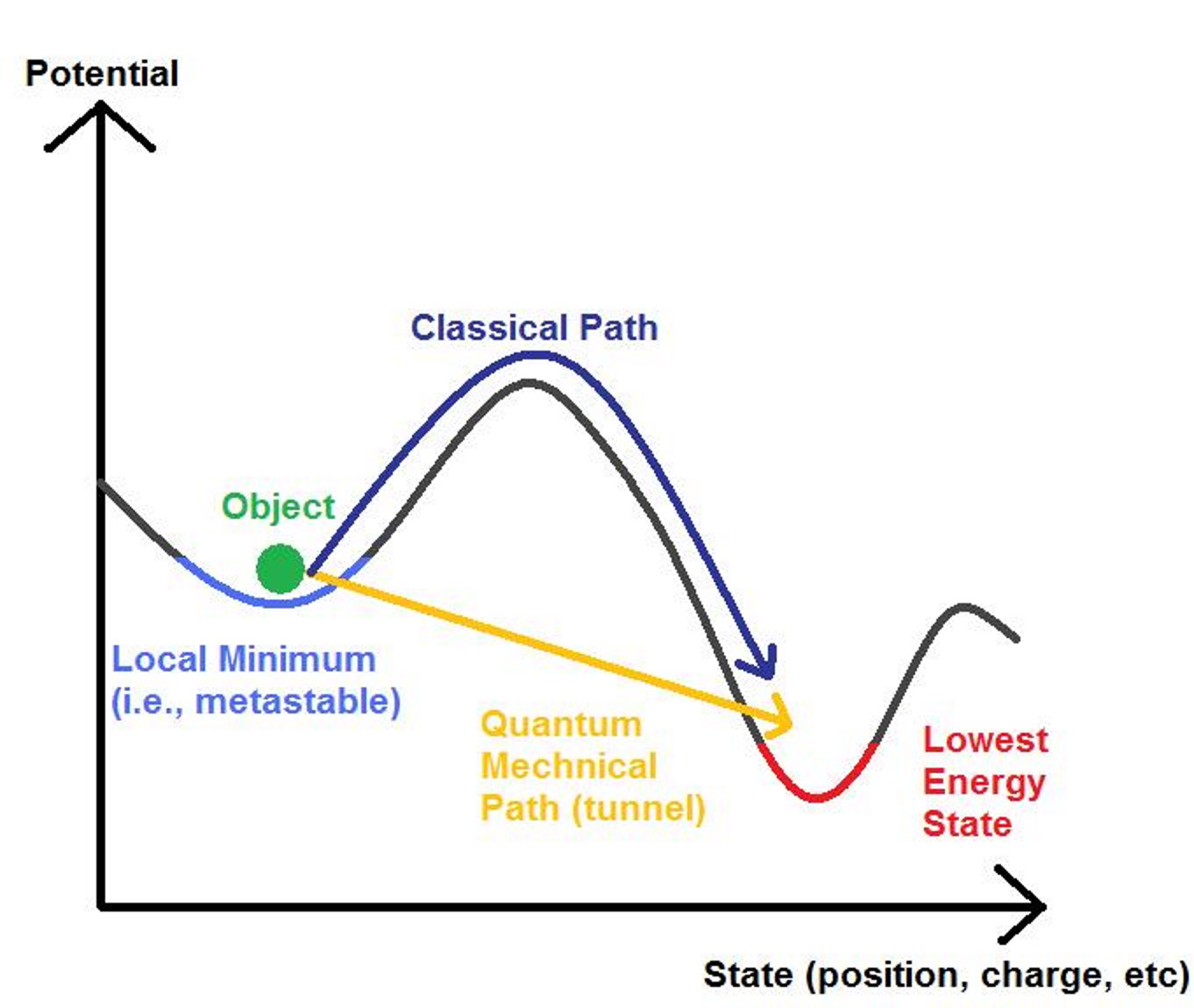
In classical physics, if you get trapped in one of these “false minima,” or a low-point that isn’t the lowest possible configuration, you’ll be stuck there unless something comes along to give that ball enough energy to rise above the boundaries of the pit it’s in. Only then will it have the opportunity to begin its descent down the hill anew, with the potential to eventually make it to a lower-energy configuration, possibly winding up in the lowest-energy (ground) state of all. This explains why balls rolling down a hill can wind up in a high-elevation depression, rather than all coming to rest in the valley down at the hill’s bottom.
But in quantum physics, you don’t need to add energy for that transition to become possible. Instead, in the quantum Universe, it’s possible to spontaneously jump from one of those false minimum states to a lower-energy configuration — even directly into the ground state — without any external energy at all. This phenomenon, known as quantum tunneling, is a probabilistic process. If the laws of nature don’t explicitly forbid such a process from occurring, then it most definitely will occur. The only question we need to answer is, “How long will it take?”

In general, there are a few main factors that determine how long an unstable (or quasi-stable) state will last.
- What is the energy difference between the reactants and the products? (Bigger differences, and bigger percentage differences, translate into shorter lifetimes for the initial state.)
- How strongly suppressed is the transition from your current state to the final state? (I.e., what’s the magnitude of the energy barrier? Larger barriers means longer lifetimes.)
- How many “steps” does it take to get from the initial state to the final state? (Fewer steps generally lead to a more likely transition, as a single decay often proceeds more quickly than a decay chain.)
- And what is the nature of the quantum pathway that gets you there? (A decay that relies on the strong nuclear force generally proceeds more quickly than a decay that relies on the weak nuclear force, for example.)
A particle like a free neutron is unstable, as it can undergo β-decay, transitioning to a proton, an electron, and an anti-electron neutrino. (Technically, it’s one of the down quarks inside the neutron that β-decays into an up quark.) A different quantum particle, the muon, is also unstable and also undergoes β-decay, transitioning to an electron, an anti-electron neutrino, and a muon neutrino. They’re both weak decays, and both mediated by the same gauge boson.
But because the products of neutron decay are 99.9% the mass of the reactants, while the products of muon decay are only ~0.05% of the reactants, the muon’s mean lifetime is measured at about ~2.2 microseconds, while a free neutron lives for about ~15 minutes.

That’s why you have to understand how impressive the discovery of bismuth’s inherent instability was. If a particle is short-lived compared to the duration of a laboratory experiment, it’s very easy to observe these particles one-at-a-time and measure how long each one lives. You can then take a large number of these measurements and determine properties like the half-life or mean lifetimes of this particular species of particle.
But for particles that live for extremely long times — longer even than the age of the Universe — that approach won’t work. If you took a particle like bismuth-209, and waited for the entire age of the Universe (~13.8 billion years), there’s less than a 1-in-a-billion chance that it would decay. It’s a terrible approach that’s completely impractical for this type of long-lived particle.
But if you took an enormous number of bismuth-209 particles, like Avogadro’s number of them (6.02 × 1023), then after one year had passed, a little more than 30,000 of them would have decayed away: via α-decay, to thallium-205, which is stable. If your experiment was sensitive enough to measure that tiny change in the atomic composition of your sample, you’d be able to detect and quantify just how unstable bismuth-209 is. We now know it to have a half-life of 2.01 × 1019 years: the longest-lived unstable element known. (Although tellurium-128 and tellurium-130 have even longer lifetimes, double-β-decaying into xenon-128 and xenon-130 with lifetimes of 2.2 × 1024 and 8.2 × 1020 years, respectively.)
You might argue, given the age of the Universe and what we use atoms for here on Earth, that for all practical purposes, perhaps we should consider bismuth to be stable. While this might be reasonable for most laboratory considerations, many of us have an insatiable curiosity about what will happen on the longest timescales of all in the Universe. Now that we know there are elements and isotopes that are unstable on extremely long timescales — timescales many times the age of the Universe, of quintillions of years or more — it’s enough to make one wonder if many of the elements that we think of as stable might, given enough time, eventually decay away.
There are presently 80 stable elements known (all of the first 82 except for technetium and promethium), with a total of 251 isotopes of those elements observed to be completely stable. However, most scientists generally agree that with longer-baselines of observation, or with more precise experiments involving large numbers of atomic nuclei, many of these elements and isotopes might be shown to eventually decay into other, more energetically favorable configurations. Some of these, like tantalum-180m (a metastable state of tantalum-180, with 73 protons and 107 neutrons) are strongly suspected to be unstable on theoretical grounds, but thus far, have never been observed to decay.
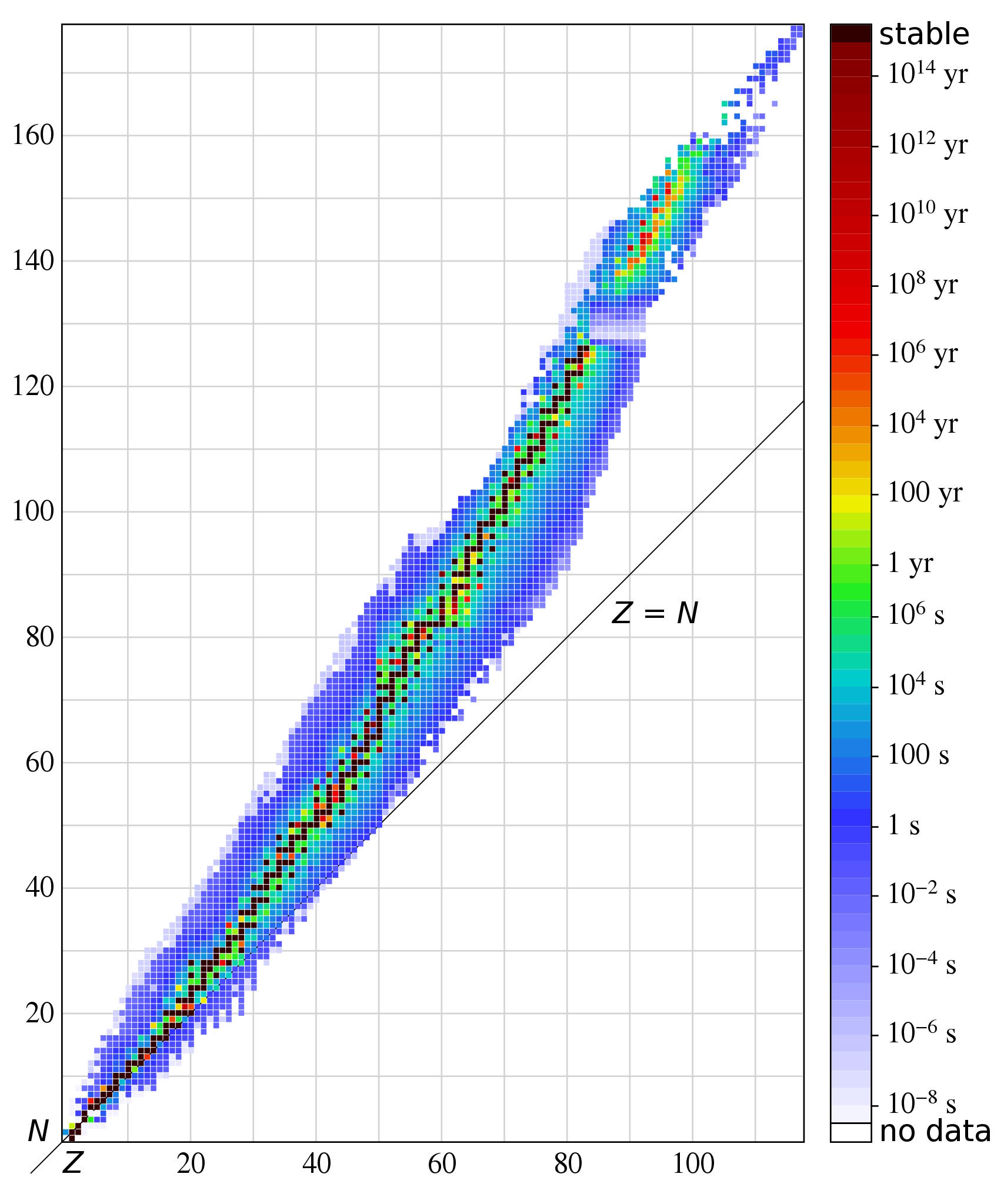
How many of the elements and isotopes that we presently think are stable today, then, will someday be shown to be inherently unstable? Believe it or not, this is one of the great open questions in science. The heaviest stable element, lead, has four known stable isotopes, including lead-208: the most abundant naturally occurring form of lead. How many of them are truly stable?
In nuclear physics there are what’s known as magic numbers: numbers that correspond to how many nucleons of any type (protons or neutrons) can be arranged into complete, filled “shells” within the atomic nucleus. (Just as electrons form shells within an atom, nucleons form shells within a nucleus.) The known magic numbers are:
- 2,
- 8,
- 20,
- 28,
- 50,
- 82,
- and 126,
with lead-208 being remarkable for being a doubly magic nucleus: with 82 protons and 126 neutrons. Some doubly magic nuclei are incredibly stable, such as lead-208, helium-4, oxygen-16, and calcium-40. But are they truly stable if we wait long enough: googols of years or even longer? Are any of the known elements truly stable if we wait long enough, or will anything containing protons and neutrons eventually decay away?
Although the frontiers of physics typically involve subatomic particles more fundamental than protons or neutrons, the far future fate of our Universe depends on the still-unknown answers to these questions. As the 21st century continues to progress, we can expect the number of known, stable isotopes to decrease from its current value of 251. But how far it will decrease is a question that only future studies can answer.