This One Puzzle Brought Physicists From Special To General Relativity

Even though it was the crowning achievement of Einstein’s career, he was only a small part of the full story.

If you were a physicist in the early 20th century, there would have been no shortage of mysteries for you to ponder. Newton’s ideas about the Universe — about optics and light, about motion and mechanics, and about gravitation — had been incredibly successful under most circumstances, but were facing doubts and challenges like never before.

Back in the 1800s, light was demonstrated to have wave-like properties: to interfere and diffract. But it also had particle-like properties, as it could scatter off of and even impart energy to electrons; light couldn’t be the “corpuscle” that Newton had imagined. Newtonian mechanics broke down at high speeds, as Special Relativity caused lengths to contract and time to dilate near the speed of light. Gravitation was the last Newtonian pillar left, and Einstein shattered it in 1915 by putting forth his theory of General Relativity. There was merely one key puzzle that brought us there.

Today, owing to Einstein’s theory, we visualize spacetime as a unified entity: a four-dimensional fabric that gets curved due to the presence of matter and energy. That curved background is the stage upon which all of the particles, antiparticles, and radiation in the Universe must travel through, and the curvature of our spacetime tells that matter how to move.

This is the big idea of General Relativity, and why it’s such an upgraded idea from Special Relativity. Yes, space and time are still stitched together into a unified entity: spacetime. Yes, all massless particles travel at the speed of light relative to all observers, and all massive particles can never attain that speed. Instead, they move through the Universe seeing lengths contract, times dilating, and — in an upgrade from Special to General Relativity — seeing novel gravitational phenomena that wouldn’t appear otherwise.

These relativistic effects, over roughly the past century, have shown up in a number of spectacular places. Light redshifts or blueshifts as it moves into or out of a gravitational field, as first detected by the Pound-Rebka experiment. Gravitational waves are emitted whenever two masses move relative to one another, an effect predicted 100 years ago but only detected over the past 4 years by LIGO/Virgo.

Starlight bends when it passes close by a massive gravitational source: an effect seen in our Solar System just as robustly as it appears for distant galaxies and galaxy clusters. And, perhaps most spectacularly, the framework of General Relativity predicts that space will be curved in such a way that distant events can be seen in multiple locations at multiple different times. We’ve used this prediction to see a supernova explode multiple times in the same galaxy, a spectacular demonstration of General Relativity’s non-intuitive power.

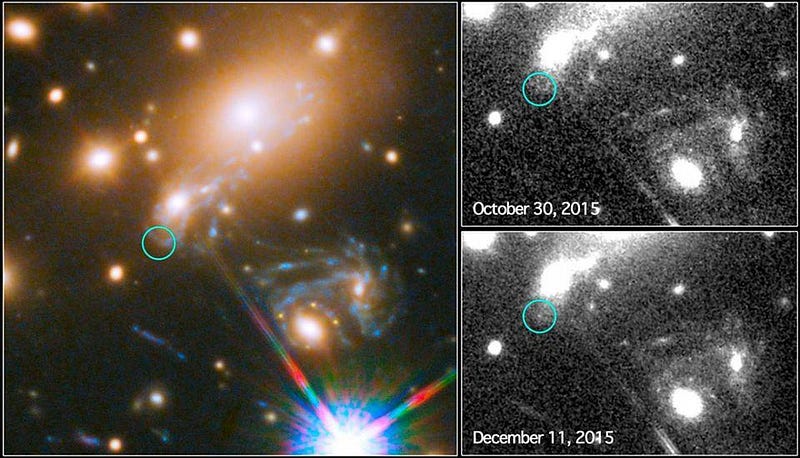
The tests mentioned above are only some of the very thorough ways General Relativity has been probed, and are far from exhaustive. But most of the observable consequences that arise in General Relativity were only worked out well after the theory itself took shape. They could not be used to motivate the formulation of General Relativity itself, but something clearly did.

If you had been a physicist in the early 20th century, you might have had an opportunity to beat Einstein to the punch. In the mid-1800s, it became clear that something was wrong with Mercury’s orbit: it wasn’t following the path that Newtonian gravity predicted. A similar problem with Uranus led to the discovery of Neptune, so many hoped that Mercury’s orbit not matching Newton’s predictions meant that a new planet must be present: one interior to Mercury’s orbit. The idea was so compelling that the planet was already pre-named: Vulcan.

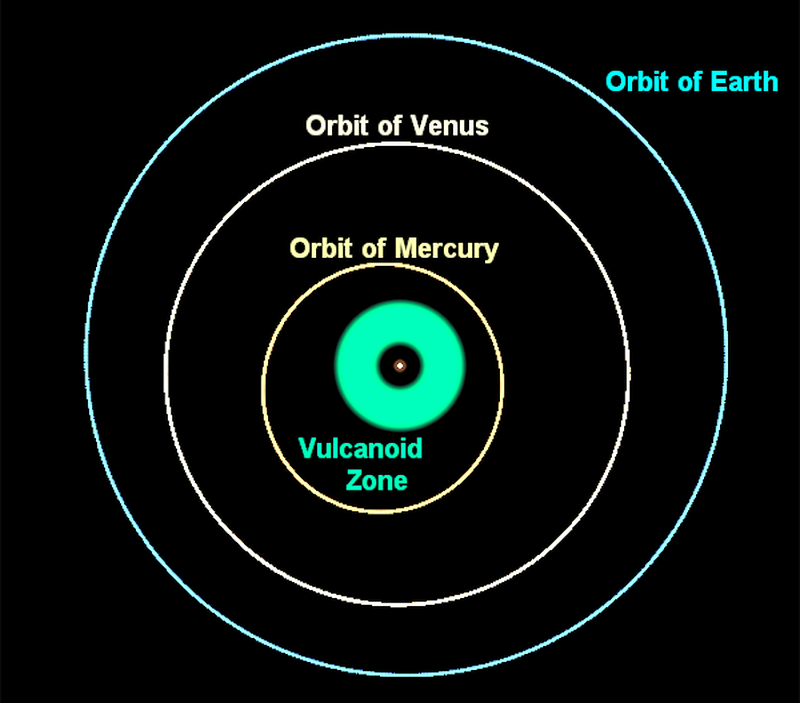
But Vulcan does not exist, as exhaustive searches quickly determined. If Newtonian gravity were perfect — i.e., if we idealize the Universe — and the Sun and Mercury were the only objects in the Solar System, then Mercury would make a perfect, closed ellipse in its orbit around the Sun.

Of course, the Universe isn’t ideal. We view the Sun-Mercury system from Earth, which itself moves in an ellipse, rotates on its axis, and sees that spin-axis precess over time. Calculate that effect, and you’ll find that the shape of Mercury’s orbital path isn’t a closed ellipse any longer, but one whose aphelion and perihelion precesses at 5025 arc-seconds (where 3600 arc-seconds is 1 degree) per century. There are also many other planets in the Solar System that tug on the Sun-Mercury system. If you calculate all of their contributions, they add an additional 532 arc-seconds per century of precession.

All told, that leads to a theoretical prediction, in Newtonian gravity, of Mercury’s perihelion precessing by 5557 arc-seconds per century. But our very good observations showed us that figure was slightly off, as we saw a precession of 5600 arc-seconds per century. That extra 43 arc-seconds per century was a nagging mystery, and the failure of searches to turn up a planet interior to Mercury deepened the puzzle even further.

It’s easy, in hindsight, to just wave our hands and claim that General Relativity provides the answer. But it wasn’t the only possible answer. We could have slightly modified Newton’s gravitational law to be slightly different from an inverse square law, and that could be responsible for the extra precession. We could have demanded that the Sun be an oblate spheroid rather than a sphere, and that could have caused the extra precession. Other observational constraints ruled these scenarios out, however, just like they ruled out the Vulcan scenario.

But sometimes, theoretical progress can lead to even more profound theoretical progress. In 1905, Special Relativity was published, leading to an understanding that — at speeds approaching the speed of light — distances appear to contract along the direction of motion and time appears to dilate for one observer moving relative to another. In 1907/8, Einstein’s former professor, Hermann Minkowski, wrote down the first mathematical framework that unified space (3D) and time (1D) into a four-dimensional spacetime fabric.

If this was all you knew, but you were thinking about the Mercury problem, you might have a spectacular realization: that Mercury isn’t just the closest planet to the Sun, but is also the fastest-moving planet in the Solar System.

With an average speed of 47.36 km/s, Mercury moves very slow compared to the speed of light: at 0.0158% the speed of light in a vacuum. However, it moves at this speed relentlessly, every moment of every day of every year of every century. While the effects of Special Relativity might be small on typical experimental timescales, we’ve been watching the planets move for centuries.

Einstein never thought about this; he never thought to calculate the Special Relativistic effects of Mercury’s rapid motion around the Sun, and how that might impact the precession of its perihelion. But another contemporary scientist, Henri Poincaré, decided to do the calculation for himself. When he factored in length contraction and time dilation both, he found that it led to approximately another 7-to-10 arc-seconds of orbital precession per century.

This was fascinating for two reasons:

1. The contribution to the precession was literally a step in the right direction, accounting for approximately 20% of the discrepancy with an effect that must be present if the Universe obeys Special Relativity.
2. But this contribution, on its own, is not sufficient to explain the full discrepancy.

In other words, doing the Special Relativity calculation was a clue that we’re on the right track, getting closer to the answer. But all the same, it isn’t the full answer; that would require something else. As Einstein correctly surmised, that “something else” would be to concoct a theory of gravitation that also incorporated Special Relativity. It was by thinking along these lines — and following the add-ons that Minkowski and Poincaré contributed — that Einstein was at last able to formulate his equivalence principle, which led to the full-fledged theory of General Relativity.

If we had never noticed this tiny deviation of Mercury’s expected behavior from its observed behavior, there wouldn’t have been a compelling observational demand to supersede Newton’s gravity. If Poincaré had never done the calculation that demonstrated how Special Relativity applies to this orbital problem, we might never have gotten that critical hint of the solution to this paradox lying in a unification of the physics of objects in motion (relativity) with our theory of gravitation.

The realization that gravitation was just another form of acceleration was a tremendous boon to physics, but it might not have been possible without the hints that led to Einstein’s great epiphany. It’s a great lesson for us all, even today: when you see a discrepancy in the data from what you expect, it might be a harbinger of a scientific revolution. We must remain open-minded, but only through the interplay of theoretical predictions with experimental and observational results can we ever hope to take the next great leap in our understanding of this Universe.